Objetivos

Con GeoGebra no solo podemos crear construcciones geométricas que hagan la función de modelos matemáticos, sino también construcciones geométricas que hagan la función de simulaciones físicas. La animación automática nos permiten simular el paso del tiempo.

En efecto, en muchas ocasiones es posible crear modelos de la estructura básica que permite a un mecanismo cumplir con el fin para el que fue diseñado. Estas construcciones son particularmente notables por mostrar el uso que se hace de las propiedades geométricas para conseguir un objetivo funcional. A su vez, el estudio de esas propiedades resulta para muchos alumnos más atractivo si aparecen relacionadas con un propósito específico y  práctico.

En esta actividad mostraremos un ejemplo. Se trata del esquema de funcionamiento de un mecanismo de barras, un triángulo de base variable. Este mecanismo se usa en la práctica en algunos tipos de gatos elevadores, balancines, puertas levadizas y otras construcciones mecánicas.

Herramientas y comandos

Usaremos las siguientes herramientas:

	Punto		Intersección		Centro
	Recta		Segmento		Semirrecta
	Circunferencia radio		Lugar		Texto

Construcción paso a paso

Antes de empezar, puede ser buena idea echar un vistazo al "Ejemplo de construcción" que se encuentra en esta página. Incluso podemos ayudarnos de la Barra de Navegación para realizar un rápido recorrido por los pasos.

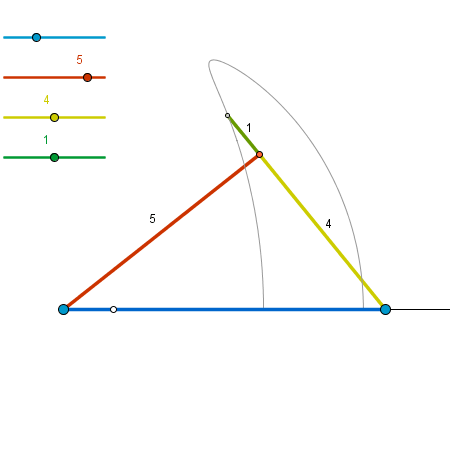
Primero crearemos cuatro deslizadores, uno para el tiempo (t) y tres para las distintas medidas (a, b y k).

Crearemos un punto A y una recta horizontal que pase por él. Colocaremos un punto C en esa recta. Después, llevaremos las medidas de los deslizadores para crear el triángulo de base variable.

Ocultamos las circunferencias y mejoramos el estilo de los tres segmentos, para resaltarlos. Al mover el punto C, nos damos cuenta que más allá de ciertos valores el triángulo desaparece. Observando con más detalle, llegamos fácilmente a la conclusión de que el triángulo solo existe cuando la distancia de C a A es como mínimo a-b y como máximo a+b.

Para evitar la desaparición del triángulo, redefinimos C para situarlo en esa zona de existencia.

Alargamos (de forma controlada por el deslizador k) una de las barras y activamos el rastro del extremo de esa barra.

Por último, como siempre, intentamos mejorar en lo posible la estética de la construcción.

Ejemplo de construcción

Comentarios

En el ejemplo de construcción hemos cambiado el rastro por el lugar geométrico. Para ello, trazamos el segmento EF, colocamos un nuevo punto restringido (C') en ese segmento y volvemos a construir el triángulo basándonos en C' en vez de en C. Una vez realizado, basta usar la herramienta  Lugar para obtener el lugar geométrico que recorre el extremo de la barra cuando C' recorre el segmento EF.

También hemos colocado textos con la medida de cada segmento, posicionados en sus puntos medios.

 Investigación:

• Existen multitud de mecanismos cuyo esquema de funcionamiento corresponde a un modelo geométrico. En muchas ocasiones, son suficientemente sencillos para poder proponerlos para su análisis: osciladores, grúas, excavadoras, prensas, motores, frenos, pinzas, tijeras, ruedas, copiadoras, escobillas... También podemos proponer la propia búsqueda de estos mecanismos como una excelente y atractiva actividad abierta.