MÓDULO 11

Introducción

Producto

Tarifas

Integrales

Radiofaros

Otros modelos

 

 


Manual       Imágenes      

 
  • Inicio
  • Módulos
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
    •     

    ► 11. Conexiones matemáticas

           ► 11.4 Integrales definidas

    Objetivos

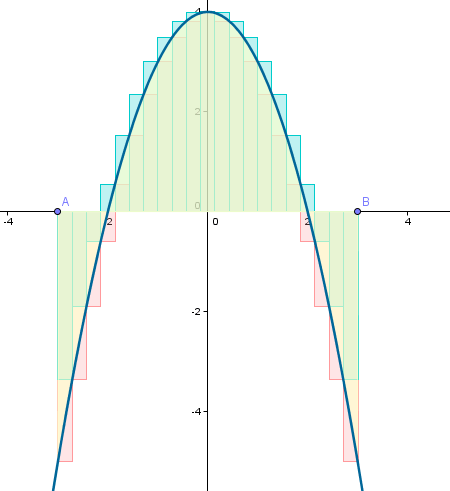
    Usaremos GeoGebra para visualizar la serie de finos rectángulos con base en el eje de abscisas y un extremo del lado opuesto en la gráfica de una función, quedando ese lado entre la gráfica de la función y el eje de abscisas. La suma de las áreas de esta serie de rectángulos converge, al tender la base de cada rectángulo a cero, al área de la superficie entre la función y el eje X.

    Esta convergencia puede observarse dinámicamente, lo que facilita en gran medida la comprensión del proceso de paso al límite. También veremos otras figuras relacionadas, como la serie superior de rectángulos, la serie de trapecios y la integral definida.

    GeoGebra incorpora varios comandos que facilitan la visualización de los conceptos correspondientes a los elementos básicos del cálculo infinitesimal. Podemos alterar tanto el intervalo en el que actuamos como la propia definición de la función, manteniendo intacta el resto de la construcción.

    También intentaremos cuidar la estética de la figura resultante y posibilitar el control de visualización de los elementos que se superpongan.

    Herramientas y comandos

    Usaremos los comandos SumaInferior, SumaSuperior, SumaTrapezoidal e Integral, y las siguientes herramientas.

    Punto Deslizador Casilla control
    Construcción paso a paso

    Antes de empezar, puede ser buena idea echar un vistazo al "Ejemplo de construcción" que se encuentra en esta página. Incluso podemos ayudarnos de la Barra de Navegación para realizar un rápido recorrido por los pasos.

    Primero prepararemos el escenario.

     Preparación

    Sí

    No

    Automático

    En el modo Automático, si mantenemos oculta la Vista Algebraica no se rotulan los objetos (ni siquiera los nuevos puntos).

    Primero determinaremos los extremos del intervalo de integración.

     Etapa 1

    • Elegir Punto y añadir dos puntos A y B haciendo sendos clic sobre dos posiciones distintas en el eje de abscisas (eje X). Asegurarse de que realmente los puntos no pueden moverse fuera de ese eje.

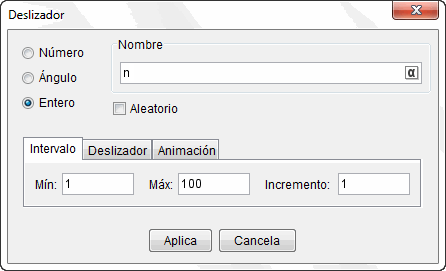
    Ahora determinaremos el número de segmentos (futuras bases de los rectángulos o trapecios) en los que dividiremos el intervalo. Queremos que ese número pueda variar entre 1 y 100.

     Etapa 2

    • Elegir  Deslizador. Clic sobre la vista gráfica. En el cuadro de diálogo que se abre, llamamos n al nuevo número, entero, y lo acotamos entre 1 y 100.

    • Escoger  Elige y mueve y arrastrar el segmento del deslizador hasta la posición que deseemos. Fijar su posición, en el cuadro de diálogo Propiedades, para evitar su arrastre accidental.
    • Mover el deslizador n hasta que alcance el valor 21.
    • Mover los puntos A y B hasta que alcancen las posiciones (-3, 0) y (3, 0) respectivamente.

    Definiremos una función.

     Etapa 3

    • Entrada: f(x) = (2+x)(2-x)

    Para facilitar su uso posterior, llamaremos a y b a las abscisas de los extremos inferior y superior.

     Etapa 4

    • Entrada: a = x(A) 
    • Entrada: b = x(B)

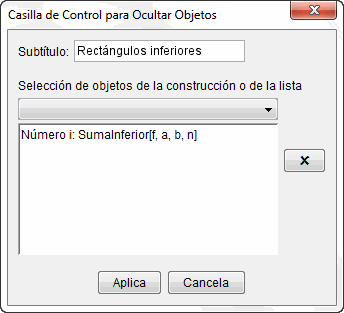
    Ahora crearemos las series y la integral definida:

     Etapa 5

    • En el Campo de Entrada, escribir (con o sin ayuda de la lista desplegable de comandos):

    i = SumaInferior [f, a, b, n]

    s = SumaSuperior [f, a, b, n]

    t = SumaTrapezoidal [f, a, b, n]

    d = Integral [f, a, b]

    Cuando introducimos un comando en el Campo de Entrada, basta pulsar F1 para conocer su sintaxis.

    Si solo nos interesan las imágenes estáticas, a medida que vamos obteniendo cada objeto gráfico (i, s, t, d) podemos enmarcarlo y exportarlo como imagen, eliminarlo (con la tecla Supr) y crear el siguiente. Con esto, finalizaríamos la actividad.

    Si, por el contrario, pretendemos crear una actividad interactiva y dinámica, podemos continuar de la siguiente manera, sin eliminar ninguno de los objetos creados.

     Etapa 6

    • Elegir  Casilla control. Clic sobre la vista gráfica. En el cuadro de diálogo emergente escribir Rectángulos Inferiores como subtítulo y elegir el número i como objeto asociado. Para ello, se puede seleccionar el objeto de la lista desplegable o, más cómodamente, hacer un simple clic sobre él, ya sea en la vista gráfica o algebraica.

    • Repetir el procedimiento con Rectángulos Superiores (s), Trapecios (t) e Integral Definida (d).
    • Escoger  Elige y mueve y arrastrar los anteriores objetos hasta la posición que deseemos. Una vez en ella, fijar las casillas en el cuadro de diálogo Propiedades, para evitar su arrastre accidental.

    Los objetos fijos deben quedar liberados antes de poder ser redefinidos.

    La visualización temporal de la Cuadrícula puede servir de ayuda en la colocación precisa de los elementos gráficos.

     Etapa 7

    • Establecer el estilo (color, grosor, opacidad...) que se considere más oportuno para los objetos creados, a través del cuadro de diálogo Propiedades.
    Ejemplo de construcción

     Integral definida

    Clic en esta imagen abre la construcción de GeoGebra

     Propuesta de construcción

    Realizar una construcción en la que se represente el área comprendida entre las gráficas de dos funciones.
    Comentarios

    Para garantizar que el valor de b=x(B) sea como mínimo el valor de a=x(A) y de ese modo evitar resultados numéricos extraños (áreas con signo negativo cuando debería ser positivo y viceversa), deberíamos haber seguido este procedimiento más cuidadoso:

     
    • Colocar el punto A en el eje X.
    • Entrada: A' = A + (1, 0)
    • Crear la  Semirrecta AA', con extremo en A.
    • Ocultar el punto A'.
    • Colocar un punto B en esa semirrecta.

     Investigación:

    • La suma superior y la suma inferior suelen diferenciarse de la integral en cantidades similares, pero distintas. ¿Tiene algo que ver este hecho con la convexidad de la función? ¿Y con el signo de la función?