MÓDULO 10

► 10. Salta a la vista

► 10.2 La media

Objetivos

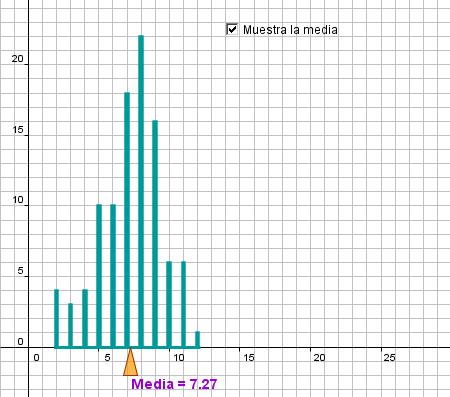
Usaremos GeoGebra para generar varios diagramas de barras correspondientes a un mismo experimento aleatorio. En concreto, cada diagrama deberá representar el resultado obtenido por la repetición (100 veces) del lanzamiento de dos dados. En cada lanzamiento, el resultado del experimento será la suma de los valores mostrados por las caras superiores de los dados.

Cada vez que queramos un nuevo diagrama, bastará con pulsar F9 (o, alternativamente, la opción del Menú Vista Recálculo de Todos los Objetos). Este procedimiento obliga a GeoGebra a recalcular todos los números aleatorios.

Como es habitual, retocaremos a nuestro gusto el estilo de los objetos gráficos.

Herramientas y comandos

Usaremos el comando Secuencia para crear rápidamente listas numéricas. Además, veremos los comandos Esquina, AleatorioEntre, CuentaSi, Barras, Media y Polígono (cuya herramienta asociada ya habíamos visto).

Usaremos la herramienta Texto para visualizar el valor de una medida estadística en la vista gráfica.

Texto

Casilla control

Construcción paso a paso

Antes de empezar, puede ser buena idea echar un vistazo al "Ejemplo de construcción" que se encuentra en esta página.

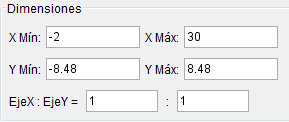
Primero prepararemos el escenario.

Preparación

Sí

Sí

Automático

En Configuración Propiedades de la vista gráfica (accesible en el Menú Opciones y también con clic derecho sobre la vista gráfica), establecer el mínimo valor del eje X en -2 y el máximo en 70. En el eje Y, establecer el mínimo en -30 y el máximo en 30. Conservar la escala 1:1 entre los Ejes X e Y (esto provocará un nuevo reajuste automático del mínimo y máximo del eje Y).

Puede ser que estos valores se necesiten ajustar posteriormente, pues depende del tamaño que posea la vista gráfica en el momento del ajuste (ancho y alto de la vista, resolución del monitor). En nuestro caso, hemos trabajado manteniendo visible la vista algebraica en un monitor configurado a 1920x1080.

En el ejemplo de construcción se puede apreciar cuál debe ser aproximadamente la escala. Los valores por defecto dependen de las dimensiones de la ventana, y son tales que el origen de coordenadas siempre quede visible en la vista estándar. Las coordenadas de las esquinas se pueden visualizar en la vista algebraica escribiendo en el Campo de Entrada el comando Esquina[4] (superior izquierda) y Esquina[2] (inferior derecha).

Ahora crearemos la lista con las sumas posibles que se pueden obtener al lanzar dos dados. Para ellos podríamos escribir, simplemente, la siguiente lista de posibilidades:

Datos = {2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}

Sin embargo, en vez de eso usaremos el comando Secuencia.

Etapa 1

Entrada: Datos = Secuencia [s, s, 2, 12]

La expresión anterior crea una lista que va recorriendo los valores de la primera expresión (que en este caso es simplemente el parámetro) cuando el parámetro s varía entre 2 y 12 (con incremento 1, por defecto) en cada paso. Por supuesto, el parámetro "s" puede tener cualquier otro nombre.

Ahora queremos simular 100 lanzamientos de los dados y obtener las 100 sumas resultantes.

Etapa 2

Entrada:

Dado1 = Secuencia [AleatorioEntre[1, 6], s, 1, 100]

Dado2 = Secuencia [AleatorioEntre[1, 6], s, 1, 100]

Cada una de las expresiones anteriores crea una lista con 100 elementos. Cada elemento, es un entero aleatorio entre 1 y 6. El resultado de cada lanzamiento corresponde a la suma de cada uno de estos pares de números.

Etapa 3

Entrada: Suma = Dado1 + Dado2

Ya tenemos la lista de resultados. Ahora vamos a agruparlos por frecuencias. La siguiente instrucción cuenta cuántos resultados de la lista Suma son iguales a 2, cuántos iguales a 3,..., cuántos iguales a 12. Observemos que la variable "x" que aparece simplemente recorre los valores de los elementos de la lista Suma (la letra de la variable de recuento, "x", está prefijada, no puede ser otra).

Etapa 4

Entrada:

Frecuencias = Secuencia [CuentaSi[x == s, Suma], s, 2, 12]

Por último, crearemos el diagrama de barras. Para ello basta usar el comando correspondiente, que trazará sobre el eje X (datos) los rectángulos de altura la frecuencia del dato y anchura la que indiquemos (0.2).

Etapa 5

Entrada: Barras = Barras [Datos, Frecuencias, 0.2]

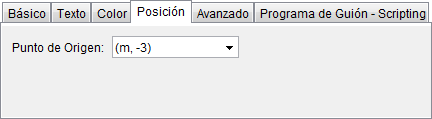
En el diagrama también podemos integrar medidas estadísticas. Como ejemplo, introduciremos la media, que señalaremos sobre el eje X mediante una "punta de flecha" triangular que nos indique su posición.

Etapa 6

Entrada:

m = Media [Suma]

Polígono [(m, 0), (m - 0.5, -2), (m + 0.5, -2)]

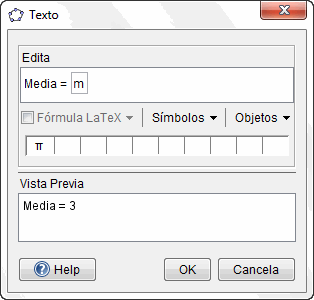
Para precisar más la información sobre la media, mostraremos su valor en la vista gráfica.

Etapa 7

Elegir Texto, hacer clic en la vista gráfica y editar el texto mixto: Media = m

Para introducir el valor de m como texto dinámico, señalarlo en la vista algebraica o elegirlo en la lista desplegable Objetos del cuadro de diálogo Texto.
Abrir el cuadro de diálogo de Propiedades de este texto y posicionar el texto en el punto (m, -3).

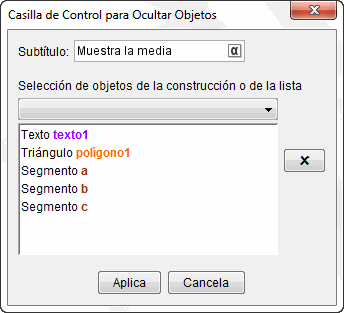
Para terminar, mejoraremos el estilo y las posibilidades de visualización.

Etapa 8

Establecer el estilo (color, grosor, opacidad...) que se considere más oportuno para los objetos creados, a través del cuadro de diálogo Propiedades.
Hacer uso de Casilla control para crear una casilla de control que permita ocultar o mostrar el texto, el polígono y los lados del polígono:

Ejemplo de construcción

Suma de dados

Clic en esta imagen abre la construcción de GeoGebra

Propuesta de construcción

Realizar una construcción similar que represente el diagrama de barras y la media correspondiente a la distribución de frecuencias absolutas del número de caras (de 0 a 5) obtenido al lanzar cinco monedas.

Comentarios

En la sección Comandos de la ayuda se puede observar que varios están dedicados específicamente al análisis de datos estadísticos, tanto de una como de dos variables, así como a la representación gráfica de los mismos.

Investigación:

Probar los distintos comandos estadísticos sobre listas de datos creadas previamente.