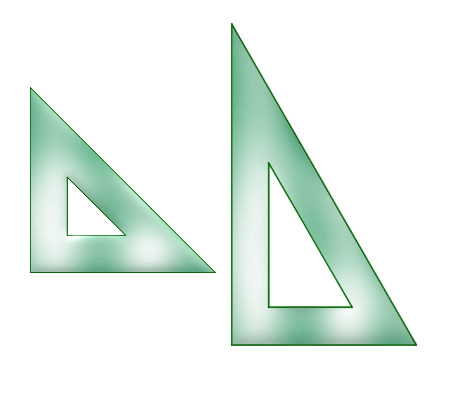Suma

En este ejemplo, la construcción plantea al azar un ejercicio aritmético y comprueba el resultado. Mientras se realiza la comprobación el usuario no puede "ensayar" otros resultados.

Clic en la imagen para abrir el applet de GeoGebra

 Eje

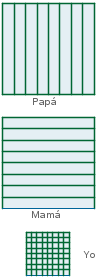
Las respuestas a las preguntas autoevaluables pueden no estar determinadas. En este ejemplo, la construcción valora positivamente cualquier diseño simétrico con respecto a un eje.

Clic en la imagen para abrir el applet de GeoGebra

 Sus + y sus -

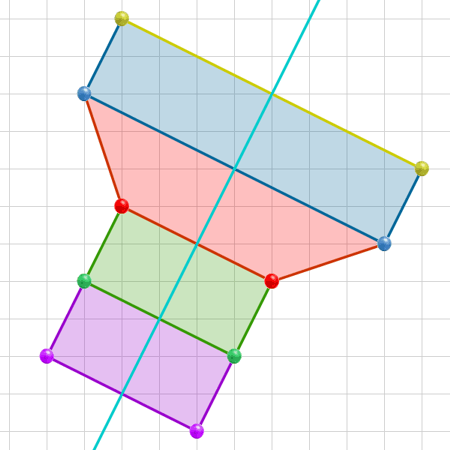
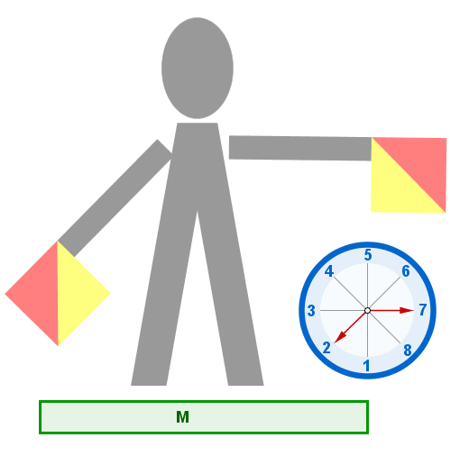
Podemos asociar un comportamiento determinado según sea la información sobre la posición de determinados objetos, lo que permite evaluar los resultados.

Clic en la imagen para abrir el applet de GeoGebra

 4x4

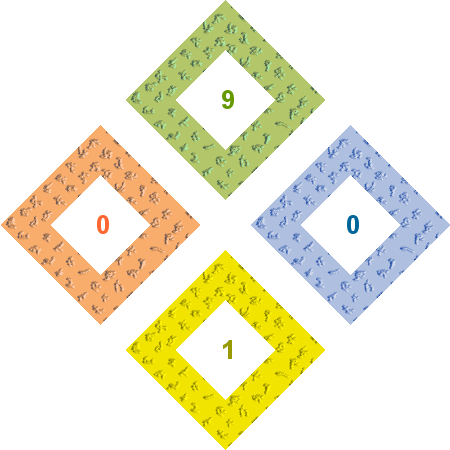
En este ejemplo la condición de visibilidad de cada número depende de la posición de un punto en un arco de la circunferencia que lo rodea. A cada posición le corresponde un valor determinado, por lo que la construcción puede evaluar si cada línea verifica o no la condición establecida.

Clic en la imagen para abrir el applet de GeoGebra

 Monosabio

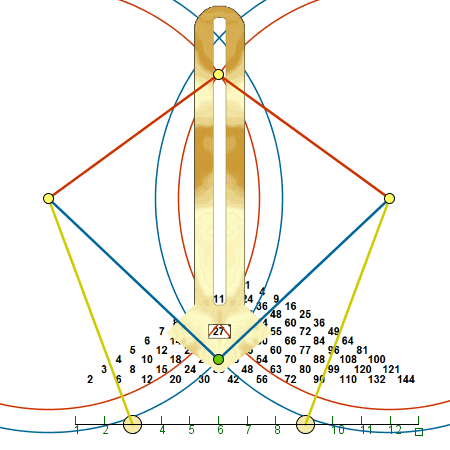
La relación entre la geometría y la aritmética, fundamental desde la matemática de la Antigua Grecia, se muestra aquí en el mecanismo de un pequeño juguete que sabe multiplicar.

Clic en la imagen para abrir el applet de GeoGebra

 Tri-ángulo

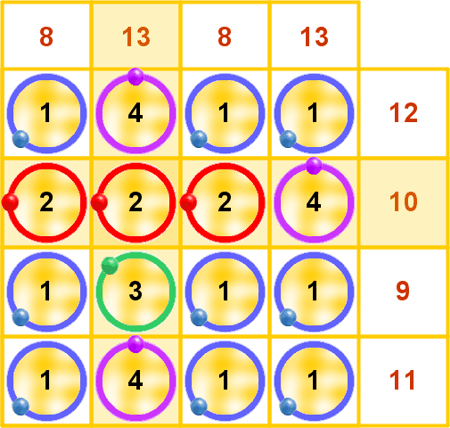
Debido a que en un mismo escenario podemos integrar escenas de distinto tipo, podemos también realizar preguntas muy diversas.

Clic en la imagen para abrir el applet de GeoGebra

 Arco iris

Los fenómenos físicos suele estar "repletos" de Matemáticas. Desde Arquímedes a Einstein, los principios que rigen el universo han necesitado el lenguaje matemático para desentrañar su naturaleza. En este ejemplo se recrea un experimento realizado por el filósofo y matemático René Descartes .

Clic en la imagen para abrir el applet de GeoGebra

 Cuadrado

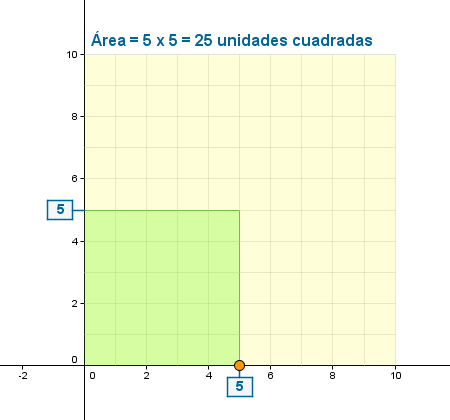
La visualización de la expresión "elevar al cuadrado", conexión entre la operación multiplicación y el área de una superficie, favorece la comprensión más profunda de ambos conceptos.

Clic en la imagen para abrir el applet de GeoGebra

 Divisores

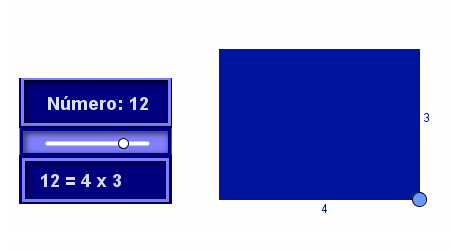
En este ejemplo se visualiza la conexión entre los divisores de un número y distintos rectángulos cuya área es ese número.

Clic en la imagen para abrir el applet de GeoGebra

 Grand Prix

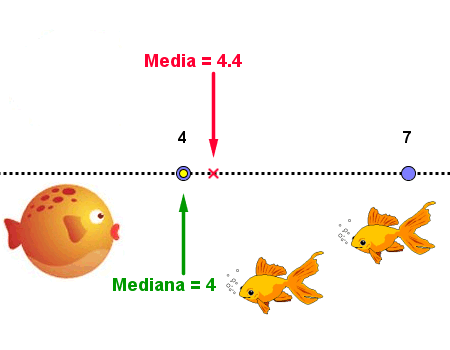
Si en las preguntas obligamos a ordenar la información, por ejemplo mediante el uso de tablas, añadimos un plus de competencia matemática al ejercitar la organización de los datos.

Clic en la imagen para abrir el applet de GeoGebra

 Regla rota

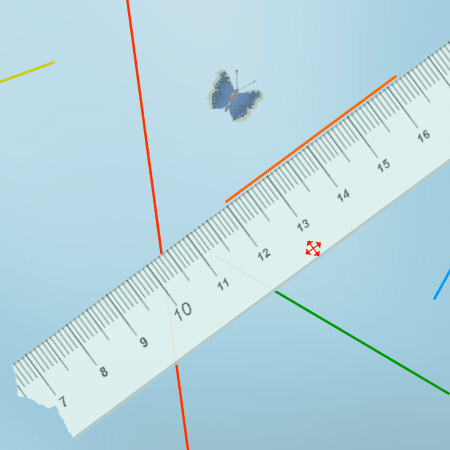
En esta actividad se relaciona la operación sustracción con el resultado de una medición.

Clic en la imagen para abrir el applet de GeoGebra

 Mediana

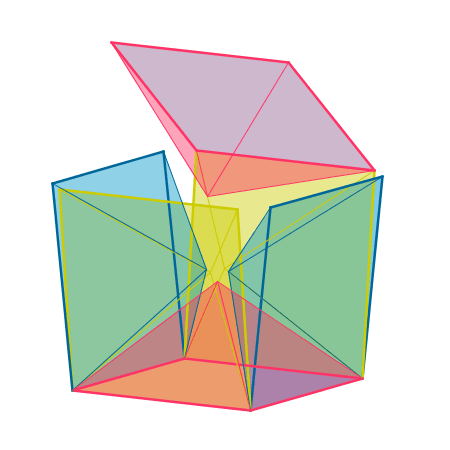
Incluso construcciones con muy pocos elementos permiten formular un gran número de preguntas, debido a las distintas posibilidades que aparecen al manipular esos elementos.

Clic en la imagen para abrir el applet de GeoGebra

 Semáforo

El uso de las está detrás de muchos lenguajes inventados por los seres humanos, desde la notación musical hasta los códigos de barras. En este ejemplo se muestra un alfabeto de señales marítimas.

Clic en la imagen para abrir el applet de GeoGebra

 Volumen

Los cuestionarios permiten desglosar una pregunta complicada en varias preguntas más sencillas. Esta estrategia se utiliza mucho en Matemáticas, tanto en la resolución de problemas como en las demostraciones formales.

Clic en la imagen para abrir el applet de GeoGebra

 Escuadras

Nota: En el applet se denomina escuadra y cartabón (en la imagen, escuadra a la izquierda y cartabón a la derecha) a esos instrumentos por ser como consta en los diccionarios actuales españoles (no en los de hace algunos años), si bien etimológicamente ambos serían "escuadras" (con el significado de "ángulo recto") y la escuadra "cartabón" sería la de la izquierda (pues cartabón significa "cuarto de círculo").

Clic en la imagen para abrir el applet de GeoGebra

 Cerezas

Una simple colección de objetos puede convertirse en un estupendo juego de estrategia pura, con un montón de variantes posibles que podemos ajustar al nivel de los alumnos.

Clic en la imagen para abrir el applet de GeoGebra