Objetivos

Usaremos GeoGebra para introducir en escena una imagen sobre la que trabajar. En este caso, queremos averiguar el área de un recorte de cartulina.

Una vez elegida una imagen y colocada como fondo de la pantalla, la Cuadrícula y las herramientas de GeoGebra nos ayudarán a realizar mediciones sobre ella.

GeoGebra facilita enormemente el trabajo sobre imágenes. Sustituir una imagen por otra es cuestión de segundos, por lo que se puede realizar la misma -o similar- actividad sobre una amplia variedad de imágenes: mapas, fotografías, vistas aéreas, pinturas, dibujos, etc. Además, sobre una misma imagen, cambiar la medición de unos puntos a otros resulta automático.

Herramientas y comandos

Usaremos las siguientes herramientas.

	Punto		Centro		Segmento
	Polígono		Circunferencia tres puntos		Imagen
	Desplaza Vista

Construcción paso a paso

Antes de empezar, puede ser buena idea echar un vistazo al "Ejemplo de construcción" que se encuentra en esta página. Incluso podemos ayudarnos de la Barra de Navegación para realizar un rápido recorrido por los pasos.

Primero prepararemos el escenario.

Insertaremos y posicionaremos una imagen. El ancho de la imagen es de 986 píxeles. Como cada unidad de los ejes cartesianos equivale (en la vista estándar) a 50 píxeles, la esquina inferior derecha la deberemos fijar 986/50 unidades más a la derecha.

Aunque asignar la segunda esquina no es imprescindible, es altamente recomendable, ya que con ello evitamos desajustes al escalar la pantalla accidentalmente usando algún tipo de zoom.

El procedimiento anterior nos garantiza que la imagen no se arrastrará accidentalmente y además conservará su tamaño relativo respecto a los Ejes y la Cuadrícula si variamos la escala de visualización haciendo zoom.

Es recomendable, en principio, que la imagen se visualice correctamente al pulsar sobre Vista Estándar (aparece en el Menú contextual de la vista gráfica, que se abre haciendo clic derecho sobre cualquier parte vacía de ella). De esta forma, se puede volver a la vista inicial rápidamente después de haber desplazado toda la vista gráfica con la herramienta  Desplaza Vista (probémoslo) o haber realizado algún tipo de zoom.

Ningún objeto debe estar seleccionado en el momento de hacer el clic derecho. Para retirar la selección de cualquier objeto, basta hacer clic sobre la vista gráfica.

Medimos el área de la cartulina creando un polígono cuyos lados coincidan con el borde.

Por último, estableceremos la escala. Para ello necesitamos la medida del diámetro de la moneda de 1 € en la fotografía. Buscando en Internet, localizamos la información relativa al diámetro real de la moneda: exactamente 2.325 cm. Basta comparar esa medida real con la medida del radio "r" en la vista gráfica para obtener la escala: 2.325/(2 r).

El valor obtenido para el área (20.61 cm²) corresponde al valor buscado.

Ejemplo de construcción

Comentarios

Por otra parte, la Cuadrícula también permite estimar el área de la cartulina. Si hacemos visible la Cuadrícula veremos que se sitúa por detrás de la imagen. Para ver la Cuadrícula a través de la imagen, establecemos la opacidad de la imagen en 50 % (Propiedades,  Estilo). 

Evidentemente, cuanto más fina sea la Cuadrícula mejor será la estimación.

Para variar la distancia entre las líneas, abrimos el Menú contextual de la vista gráfica, elegimos el cuadro de diálogo Propiedades y tildamos en la pestaña  Cuadrícula la casilla "Distancia" estableciendo la misma (0.4, por ejemplo).

Si ahora contamos (con bastante paciencia) solo las casillas que tienen la mitad o más de su superficie ocupada por la cartulina, obtenemos una cuenta de 715 casillas de 0.16 u.c. de área cada una. Esto arroja un valor del área de la cartulina prácticamente idéntico al arriba obtenido.

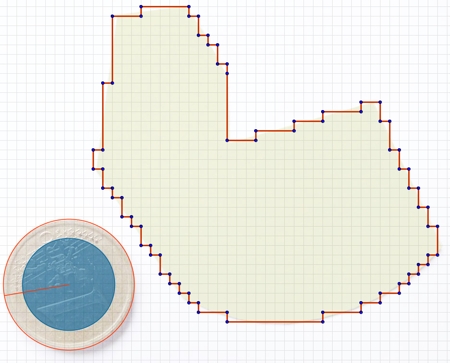
Clic en esta imagen abre la construcción de GeoGebra

 Investigación:

• Las cada vez más populares y accesibles imágenes de amplias zonas terrestres tomadas desde los satélites abren la puerta a plantear la investigación sobre la medición en la superficie esférica. Sin entrar en cálculos engorrosos, resulta interesante observar el contraste entre la geometría plana y la esférica, comparando los relaciones que se cumplen en ambas y aquellas que difieren (a veces, notablemente, como en el caso de la suma de los ángulos de un triángulo).