|

|
FACILIDAD: Geometría CAS
Distancias
Equidistancias
Distancias constantes
Ecs. algebraicas e
inecuaciones
Ángulos
Distancia del Taxi
Cuerpos
VERSATILIDAD
Listas de poligonales
FLEXIBILIDAD: Geometría elástica
Geometría elástica
Newton's Principia
Tensegridades |
Resumen
Desde su origen, GeoGebra está diseñado específicamente para mostrar la
representación dual, gráfica y algebraica, de los objetos matemáticos. En
esta presentación, como eje central, mostraré algunos procedimientos que
explotan las posibilidades didácticas de esta dualidad.
Estos
procedimientos, expuestos a estudiantes de 15 o 16 años, son tan sencillos,
atractivos y rápidos de crear que permiten que sean los propios alumnos y
alumnas
quienes los generen y utilicen desde cero... ¡con todo éxito!
A pesar de su
sencillez, veremos que son tan poderosos que nos permiten bucear en
profundidades matemáticas prácticamente inabordables en el aula de
secundaria sin la ayuda de GeoGebra, desde estructuras algebraicas (como los
cuerpos) hasta métricas no euclídeas (como la taxicab). |
Nota:
Todas las construcciones GeoGebra enlazadas en esta página web han sido
realizadas por quien aquí las presenta.
Ninguna de ella, salvo la construcción Burbujas, hace uso de programación JavaScript.
El autor
Mi relación con GeoGebra se remonta a 2005, año en que conocí este
programa creado por Markus Hohenwarter [7],
aunque ya había trabajado con otros programas de geometría dinámica. Dos
años después, en 2007, el profesor Tomás Recio
 me convoca al Centro
Internacional de Encuentros Matemáticos (CIEM me convoca al Centro
Internacional de Encuentros Matemáticos (CIEM
 , Cantabria) que reunió,
entre otros, a
varios profesores de secundaria españoles pioneros en el uso
didáctico de la geometría dinámica. En esa reunión defendí la eficiencia
de GeoGebra [10] frente a otros programas como Cabri.
Una consecuencia de ese
encuentro fue la formación del grupo G⁴D , Cantabria) que reunió,
entre otros, a
varios profesores de secundaria españoles pioneros en el uso
didáctico de la geometría dinámica. En esa reunión defendí la eficiencia
de GeoGebra [10] frente a otros programas como Cabri.
Una consecuencia de ese
encuentro fue la formación del grupo G⁴D  ,
constituido por J.M. Arranz ,
constituido por J.M. Arranz  , J.A. Mora , J.A. Mora  , M. Sada , M. Sada  y el que esto escribe
y el que esto escribe
 . .
Dos años más tarde, desde el Ministerio de Educación de España,
Antonio Pérez  ,
entonces director del Instituto de Tecnologías
Educativas (ITE, hoy INTEF ,
entonces director del Instituto de Tecnologías
Educativas (ITE, hoy INTEF  ),
me encarga la realización de cursos para la formación en GeoGebra del profesorado de Educación Primaria y Secundaria [11,
13], así como la creación de
un conjunto de actividades completas (introducción del tema, construcción
a explorar y cuestionario) para el alumnado, clasificadas por temas y
niveles, que bautizamos como Proyecto Gauss [14,
1]. Simultáneamente, Tomás pone en
marcha el
primer Instituto GeoGebra en lengua española, el Instituto GeoGebra de
Cantabria ),
me encarga la realización de cursos para la formación en GeoGebra del profesorado de Educación Primaria y Secundaria [11,
13], así como la creación de
un conjunto de actividades completas (introducción del tema, construcción
a explorar y cuestionario) para el alumnado, clasificadas por temas y
niveles, que bautizamos como Proyecto Gauss [14,
1]. Simultáneamente, Tomás pone en
marcha el
primer Instituto GeoGebra en lengua española, el Instituto GeoGebra de
Cantabria  , del cual soy Formador
desde su creación. , del cual soy Formador
desde su creación.
Introducción
El objetivo principal de esta conferencia es mostrar la estrecha relación entre los
procedimientos algebraicos y geométricos usando GeoGebra. Una gran parte del
tiempo lo dedicaré a presentar actividades que pueden ser abordadas por
estudiantes de educación secundaria mediante construcciones realizadas por
sí mismos. Al
margen de que se pueden emplear de modo esporádico para explorar algunos
contenidos específicos, este tipo de construcciones adquiere toda su potencia didáctica
en una enseñanza de las matemáticas basada en la adquisición de
competencias.
En la primera parte de esta presentación detallaré procedimientos muy
sencillos que aprovechan la fuerte interconexión entre geometría y álgebra
que da nombre a GeoGebra (de ahí el título de Principia)
y permiten proponer a
estudiantes de enseñanza secundaria (de unos 15 o 16 años) exploraciones matemáticas
"en principio" fuera de su alcance, dejando a las poderosas herramientas de GeoGebra
el pesado cálculo algebraico y geométrico, del mismo modo que dejamos actualmente a las
calculadoras y hojas de cálculo el pesado y aburrido cálculo aritmético.
En particular, la facilidad con la que podemos crear rectas y
circunferencias paralelas nos ayudará a construir un offset
dinámico cuyo rastro de color permitirá visualizar una gran variedad de
lugares geométricos. Al mismo tiempo, el CAS, aplicado a las distancias
euclídeas,
nos facilitará la creación de curvas implícitas que se ajusten a esos
lugares. También veremos cómo convertir, en ocasiones, esas curvas
implícitas en ecuaciones e inecuaciones.
Ampliaremos el uso del CAS a ángulos y también
abordaremos otras distancias no euclídeas, como la distancia del Taxi.
Finalizaremos esta primera parte con un ejemplo recíproco, en el que
recurrir a la geometría nos facilitará la visualización y manipulación
de los conceptos y propiedades inherentes a la estructura algebraica de
cuerpo.
En la segunda parte, mostraré algunas ideas para realizar construcciones
algo más sofisticadas, pero no menos atractivas, que pueden servir de modelo para ser analizadas o
modificadas por el alumnado.
Primero veremos cómo las listas de GeoGebra facilitan la
incorporación de gran
cantidad de información. Como ejemplo, representaremos la línea costera de
los continentes en una única lista, obteniendo una plantilla de la Tierra.
A continuación usaremos los vectores para modificar en todo instante
(gracias a los guiones de GeoGebra) la posición de los puntos de acuerdo
con nuestros intereses. Estos vectores pueden usarse para combinar fuerzas
repulsivas (como partículas del mismo signo), atractivas (como las usadas
por
Newton para formular su ley de gravitación universal) o simplemente
reactivas (como las del choque elástico).
Es más, podemos usar los vectores para crear una "geometría elástica".
En ella, los puntos no poseen un emplazamiento definido sino que su posición
en cada instante es el resultado de la aplicación de las fuerzas
mencionadas. Así, por ejemplo, en la geometría elástica un punto no "está" en una circunferencia,
sino que es irremediablemente atraído por ella, tiene "su límite" en ella.
Por último, como aplicación de este tipo de geometría elástica, veremos
ejemplos de construcción de tensegridades.
FACILIDAD: Geometría CAS
GeoGebra: Geometría y Álgebra
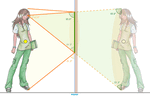
Desde su nacimiento, GeoGebra permite la construcción rápida y sencilla de
modelos geométricos, lo que facilita tanto el aprendizaje como la
enseñanza y la investigación. Esta facilidad
favorece el efecto IKEA
 (valoramos más lo que
somos capaces de construir nosotros mismos, de ahí el éxito de los juegos clásicos de
construcción, como el Meccano o el Lego). Aquí se
muestra una de las construcciones que presenté en la reunión de 2007 en el
CIEM [9]
y con las que defendí el uso de este programa en la enseñanza. He elegido
esta porque Markus la
popularizó al mantenerla durante años como parte de la cabecera de la web
oficial de GeoGebra (valoramos más lo que
somos capaces de construir nosotros mismos, de ahí el éxito de los juegos clásicos de
construcción, como el Meccano o el Lego). Aquí se
muestra una de las construcciones que presenté en la reunión de 2007 en el
CIEM [9]
y con las que defendí el uso de este programa en la enseñanza. He elegido
esta porque Markus la
popularizó al mantenerla durante años como parte de la cabecera de la web
oficial de GeoGebra
 . .
Desde entonces, GeoGebra se ha desarrollado enormemente. Podemos construir
una infinidad de modelos y aplicaciones, relacionadas con áreas como, por
ejemplo, Aritmética, Ecuaciones, Funciones, Isometrías, Variable compleja, Estadística, Probabilidad, Juegos o incluso Música
 . .
La variedad de procedimientos también es enorme: desde cortar un hipercubo
en lonchas [15] hasta demostrar
automáticamente una proposición [12,
17, 18, 28].
Resulta evidente que lo que caracteriza a la geometría dinámica es
precisamente su dinamismo. Al igual que en la mayoría de los animales que
poseen un sistema visual, la evolución ha provocado que se dispare
una alerta mental cuando cualquier objeto o ser en nuestro entorno se pone
en movimiento. Por tanto, el movimiento es un natural y excelente medio
para focalizar la atención.
Sin embargo, ¿cómo
podemos visualizar fácilmente lugares geométricos sin recurrir a
construcciones complejas ni usar farragosas ecuaciones algebraicas?
Veremos que una posible respuesta es usar el CAS.
Distancias
El concepto matemático sobre el que gravitaré es un concepto fundamental: la
distancia.
|
Al colocar un punto en un espacio, el concepto de
distancia a él se comporta como lo que los físicos llaman "campo": no se
manifiesta hasta que introducimos otro objeto en él.
Emplearemos dos procedimientos sencillos para visualizar lugares
geométricos relacionados con la distancia: la creación de curvas implícitas y el uso del
offset dinámico con rastro activado. |
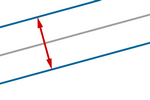
Método clásico: secuencias de curvas paralelas (offset
estático)
Usando el comando VectorNormalUnitario (y su vector opuesto), es
sencillo crear secuencias de paralelas a una recta, a distancias
progresivas. Para cada
recta r, encontramos un par de secuencias:
Secuencia(Traslada(r, k VectorNormalUnitario(r)),
k, 0, 20, 0.2)
Secuencia(Traslada(r, –k VectorNormalUnitario(r)),
k, 0, 20, 0.2)
Gracias al comando VectorCurvatura y a la
herramienta Lugar geométrico, podemos generalizar el paralelismo a
muchas curvas (offset  ).
Si P es un punto de la curva c, las dos curvas paralelas a
distancia k vendrán dadas por el lugar geométrico de los puntos: ).
Si P es un punto de la curva c, las dos curvas paralelas a
distancia k vendrán dadas por el lugar geométrico de los puntos:
P ± k VectorUnitario(VectorCurvatura(P, c))
Observemos que, en general,
las curvas offset no
son congruentes con la curva original. Es decir, las curvas paralelas no
son simples traslaciones, salvo que se trate de rectas.
Pero, en el caso de la circunferencia (pongamos de centro O y radio
4), cuyo offset también
es una circunferencia, no necesitamos ni el comando VectorCurvatura ni
la herramienta Lugar geométrico, ya que basta variar
adecuadamente el radio de la circunferencia original:
Secuencia(Circunferencia(O, 4 + k), k, 0, 20,
0.2)
Secuencia(Circunferencia(O, 4 – k), k, 0, 20,
0.2)
Además, si consideramos un punto O como una circunferencia de radio 0,
obtenemos una única secuencia de offsets centrados en él:
Secuencia(Circunferencia(O, k), k, 0, 20,
0.2)
|
Resumiendo: podemos crear
fácilmente secuencias de paralelas a rectas, circunferencias y puntos. |
Offset dinámico con rastro activado
Ahora sustituiremos cada secuencia de paralelas por una única paralela
dinámica.
Como antes, usando el comando VectorNormalUnitario (y su vector opuesto), es
sencillo crear paralelas a una recta, a una distancia d dada.
Para cada
recta r, encontramos un par de paralelas:
Traslada(r, d VectorNormalUnitario(r))
Traslada(r, –d VectorNormalUnitario(r))
Gracias al comando VectorCurvatura y a la
herramienta Lugar geométrico, podemos generalizar el paralelismo a
muchas curvas (offset). Si P es un punto de la curva c,
las dos curvas paralelas a distancia d vendrán dadas por el lugar
geométrico de los puntos:
P ± d VectorUnitario(VectorCurvatura(P, c))
Observemos que, en general, las curvas offset no
son congruentes con la curva original. Es decir, las curvas paralelas no
son simples traslaciones, salvo que se trate de rectas.
Pero, en el caso de la circunferencia (pongamos de centro O y radio
4), cuyo offset también
es una circunferencia, no necesitamos ni el comando VectorCurvatura ni
la herramienta Lugar geométrico, ya que basta variar
adecuadamente el radio de la circunferencia original:
Circunferencia(O, 4 + d)
Circunferencia(O, 4 – d)
Además, si consideramos un punto O como una circunferencia de radio 0,
obtenemos un único offset centrado en él:
Circunferencia(O, d)
|
Resumiendo: podemos crear
muy fácilmente offsets de rectas, circunferencias y puntos. |
También podemos crear los puntos de intersección de dos objetos y el
Lugar Geométrico (Locus) correspondiente. El problema del empleo del
comando o la herramienta Lugar Geométrico es que en muchas situaciones
(más complicadas que la mostrada aquí) no es posible usarlo adecuadamente.
Como GeoGebra es un programa de Geometría Dinámica, no solo podemos mover
los objetos geométricos a nuestro antojo: también podemos establecer
animaciones automáticas [22].
Para ello, añadimos rastro al offset y
elegimos un valor d decreciente (opuesto a un deslizador "incrementando
una sola vez"). Nota: alternativamente, podemos elegir un valor
d
creciente (incrementando una sola vez) y asignarle como velocidad -1 en
vez de 1.
Así, haciendo offset simultáneamente sobre un punto y una recta,
por ejemplo, podemos visualizar la parábola por contraste de color.
|
La ventaja del offset frente a la curva implícita,
que veremos a continuación, es
que nos permite detener en cualquier momento la reproducción del
procedimiento y observar cómo se cortan los rastros de las líneas para
entender por qué esos puntos de corte forman parte del lugar geométrico
buscado. |
Curvas implícitas desde definiciones en CAS

Una parábola se puede definir como el lugar
geométrico de los puntos del plano que equidistan de una recta
(directriz) y un punto exterior a ella (foco). Localizar un punto (el
vértice) es fácil, pero, ¿cómo localizar los demás?
Con GeoGebra, podemos crear un punto libre con el que tantear el terreno, y
marcar aquellas posiciones en donde se igualen las distancias. Es un
trabajo muy didáctico, pero después de varios ejercicios llega a resultar tedioso.
Alternativamente, podemos construir un punto genérico que cree el lugar
geométrico, pero esta construcción solo servirá para este caso o
similares.
También podemos crear la curva implícita definiendo
en la Vista CAS un punto arbitrario X(x,y):
X:= (x, y)
la distancia de X al foco F:
XF(x,y):= Distancia(X, F)
la distancia de X a la directriz r:
Xr(x,y):= Distancia(X, r)
e igualando ambas distancias:
XF – Xr = 0
GeoGebra usa algoritmos numéricos para crear esta curva implícita, por lo
que en algunos casos pueden aparecer pequeños errores u omisiones.
Nota: Al menos de momento, GeoGebra no representa ecuaciones de este tipo
en tres variables. Es decir, reconoce x² + y² + z² = 16 como una esfera, pero no
reconoce como tal la ecuación equivalente (sqrt(x² + y² + z²))² = 16.
Equidistancias
Ahora solo tenemos que usar esas sencillas herramientas para investigar
con su ayuda toda una variedad de situaciones.
En lo sucesivo, consideramos definidas las distancias de un punto
arbitrario X(x,y) a A y B como:
XA(x,y):= Distancia(X, A)
XB(x,y):= Distancia(X, B)
a una recta r como:
Xr(x,y):= Distancia(X, r)
y a una circunferencia c como:
Xc(x,y):= Distancia(X, c)
Equidistancia a dos o tres puntos

Al contraer las circunferencias con el rastro activado, en cada punto del
plano sobrevive el color correspondiente al centro más cercano, por lo que
obtenemos la mediatriz.
La curva implícita de la mediatriz de AB tiene por ecuación:
XA – XB = 0
En el caso de tres puntos, podemos visualizar el circuncentro [2] del triángulo que determinan.
|
Ya hemos visto... |
Equidistancia a un punto y una recta

Al acercar al mismo tiempo una paralela a la recta r y a la circunferencia, centrada en
A, con el rastro activado, sobrevive el
color del objeto más cercano (recta o punto), por lo que obtenemos la
correspondiente parábola.
Como ya hemos visto, en este caso también resulta sencillo construir ese
locus.
|
Equidistancia a un punto y una circunferencia
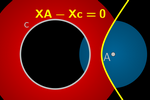
Si el punto está en el círculo, obtenemos una elipse y si está fuera, una
rama de hipérbola.
La curva implícita de la elipse o rama de la hipérbola tiene por ecuación:
XA – Xc = 0
Observemos que una construcción similar a la de la parábola también nos
permite generar ese lugar geométrico.
|
Más... |
Equidistancia a un punto y una cónica
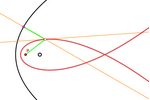
Estas construcciones de los lugares geométricos de
los puntos que equidistan de un punto y de una cónica son muy similares a la construcción de
los lugares que equidistan de un punto y una circunferencia. Sin embargo,
la ecuación es mucho más complicada de encontrar.
|
Equidistancia a dos rectas

Al acercar al mismo tiempo paralelas a dos rectas, con el rastro activado,
sobrevive el color correspondiente a la recta más cercana, obteniendo las
bisectrices.
En el caso de tres rectas, podemos visualizar el incentro y los
exincentros del triángulo que determinan.
Como caso particular, podemos visualizar el eje medio
 de un polígono como frontera (compuesta por segmentos y arcos de parábolas) entre los
rastros supervivientes.
de un polígono como frontera (compuesta por segmentos y arcos de parábolas) entre los
rastros supervivientes.
Al igual que anteriormente, también podemos visualizar y construir
fácilmente el lugar geométrico correspondiente a la bisectriz.
Equidistancia recta-circunferencia y a dos
circunferencias
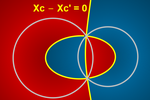
El lugar geométrico de los puntos que equidistan de
una recta y una circunferencia está formado, en general, por una parábola o, si se
cortan, dos parábolas.
El lugar geométrico de los puntos que equidistan de dos
circunferencias está formado, en general, por una rama de hipérbola o, si se
cortan, una elipse.
Diagrama de Voronoi y mapas similares

Aunque la curva implícita es más rápida de crear y usar, el método offset
permite afrontar problemas que la curva implícita no puede abordar. Por
ejemplo, si en vez de a la equidistancia entre dos puntos (mediatriz) aplicamos el
método offset a varios puntos, obtenemos el diagrama de Voronoi (o
polígonos de Thiessen).
De modo similar, podemos también crear el mapa de las regiones más
próximas a una colección de rectas o circunferencias.
Nota: El comando Voronoi de GeoGebra no colorea cada
región. Puede verse un modo dinámico de hacerlo aquí
 . .
Equidistancia a dos curvas

Podemos aplicar el método offset a dos curvas, siempre que podamos
calcular el vector normal en cada punto de ambas.
En el caso de que no podamos calcular los vectores normales, siempre
podemos crear un mapa de calor usando la técnica del escáner de color dinámico [3,
19, 26, 27,
31].
Distancias constantes
Punto-Punto
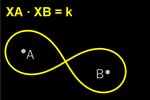
Cuando la suma de las distancias de los puntos del lugar
buscado a los puntos A y B es constante, obtenemos una elipse.
Cuando la diferencia de las distancias de los puntos
del lugar buscado a los puntos A y B es constante, obtenemos una rama de
hipérbola. (En el caso de que la constante sea 0, obtenemos la mediatriz.)
Cuando el producto de las distancias de los puntos del
lugar buscado a los puntos A y B es constante, obtenemos un óvalo de Cassini
 . Si la constante coincide con el cuadrado de la mitad de la
distancia AB, obtenemos una lemniscata de Bernoulli . Si la constante coincide con el cuadrado de la mitad de la
distancia AB, obtenemos una lemniscata de Bernoulli
 . .
Cuando el cociente de las distancias de los puntos del
lugar buscado a los puntos A y B es constante, obtenemos,
sorprendentemente
 , una
circunferencia. (En el caso de que la constante sea 1, obtenemos la
mediatriz.) , una
circunferencia. (En el caso de que la constante sea 1, obtenemos la
mediatriz.)
Cociente constante punto-recta

Cuando el cociente de las distancias de los puntos del lugar buscado
al punto A y la recta r es una constante k, obtenemos una cónica, que será
elipse, parábola o hipérbola según sea el valor de k (excentricidad)
menor, igual o mayor que 1, respectivamente
 . .
Combinación lineal constante
Podemos generalizar las sumas y diferencias a cualquier combinación lineal
de distancias entre puntos, punto y recta, punto y circunferencia, etc.
Surgen así cónicas y cuárticas (óvalos cartesianos, productos de
rectas...), el caracol de Pascal
 ,
así como curvas de grado superior producto de las anteriores. ,
así como curvas de grado superior producto de las anteriores.
|
Más... |
Combinación lineal logarítmica constante
 También podemos generalizar los productos y cocientes a cualquier
combinación lineal de logaritmos de distancias. También podemos generalizar los productos y cocientes a cualquier
combinación lineal de logaritmos de distancias.
|
Suma constante a tres o cuatro
puntos
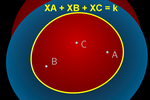 En el caso de la suma constante
k de distancias a tres puntos
A, B y C, basta con introducir:
XA + XB + XC = k
Para realizar el offset, lo que
hacemos es solapar el rastro de las elipses Elipse(A, B, (k–h)/2) con las
circunferencias Circunferencia(C, h), donde
h es un parámetro real positivo que va disminuyendo desde el valor
k hasta cero. Los
puntos frontera de color serán entonces precisamente los puntos que cumplan:
Elipse(A, B, (k–h)/2) = Circunferencia(C, h)
que es equivalente a que la suma
de distancias de esos puntos a
A, B y C sea
exactamente la cantidad prefijada k (pues XA + XB = k – h,
XC = h). Conseguimos así mostrar
una 3-elipse
 . En el caso de cuatro puntos, se solapan el rastro de dos elipses, determinando una 4-elipse. . En el caso de cuatro puntos, se solapan el rastro de dos elipses, determinando una 4-elipse.
Nota: Un enfoque algebraico de esta situación,
también con GeoGebra, puede verse
en este artículo [8] de Zoltán Kovács.
Ecs. algebraicas e inecuaciones
Equidistancia a un punto y una circunferencia:
ecuación algebraica
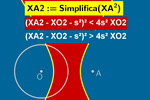
Anteriormente, habíamos definido directamente la distancia de un punto X(x,y)
a la circunferencia c como:
Xc(x,y):= Distancia(X, c)
con lo que la ecuación de los puntos equidistantes
de un punto y una cirunferencia se reduciría a:
XA – Xc = 0
Si la circunferencia tiene centro O y radio s, podemos
redefinir la ecuación anterior como:
|XO – s| = XA
Esta redefinición nos permitirá visualizar las dos ramas de la hipérbola.
Para ello, basta transformar la
anterior ecuación irracional en una ecuación algebraica, elevando al
cuadrado para eliminar las raíces (alcanzar la siguiente expresión
es fácil, pues no requiere procesos de agrupación, simplificación o
cancelación, pero tampoco pasa nada por ayudar a estudiantes
con pocos recursos algebraicos a
resolver este pequeño ejercicio, el resultado merece la pena):
(XA² – XO² – s²)² = 4s² XO²
Las ecuaciones algebraicas tienen además la ventaja de permitir
representar las correspondientes inecuaciones sin tener que recurrir al
offset. Para ello basta definir:
XA2(x,y) := Simplifica(XA^2)
XO2(x,y) := Simplifica(XO^2)
De este modo, podemos introducir las inecuaciones:
(XA2 – XO2 – s²)² < 4s² XO2
(XA2– XO2 – s²)² > 4s² XO2
Equidistancia a dos puntos: restricciones en la
representación de inecuaciones
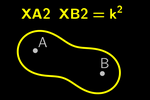
Pero no siempre la ecuación algebraica permite a GeoGebra representar las
inecuaciones correspondientes. Tal y como aparece en el manual oficial
 ,
esta representación está limitada a los siguientes casos: ,
esta representación está limitada a los siguientes casos:
-
inecuaciones polinómicas en una variable, como x³ > x + 1
-
inecuaciones cuadráticas en dos variables, como x² + y² + x y < 4
-
inecuaciones lineales en una de las variables, como 2x > sen(y)
Al hallar la ecuación algebraica correspondiente a XA – XB = k, obtenemos
la misma que la correspondiente a XA + XB = k:
4 XB2 XA2 = (k² – XA2 – XB2)²
ecuación que se reduce a una cuadrática en dos variables, lo que permite a
GeoGebra la representación de sus correspondientes inecuaciones.
Nota: la ecuación cuadrática común a la elipse y a
la hipérbola no es más que la ecuación general de la cónica
a x² + b x
y + c y² + d x + e y + f = 0
en la que la elipse y la hipérbola solo
se distinguen según el signo del discriminante b² – 4 a c.
Pero la ecuación algebraica correspondiente a XA XB = k no representa una
cónica, por lo que GeoGebra no puede representar las inecuaciones
correspondientes. En cambio, la ecuación algebraica correspondiente a XA =
k XB vuelve a ser una cónica, lo que permite a GeoGebra representar las
inecuaciones correspondientes.
Sumas iguales de distancias a dos pares de puntos

Si introducimos XA + XB = XC, el lugar geométrico resultante
corresponde a la intersección de una familia de elipses XA + XB = k, y
una de circunferencias XC = k, según varíe el parámetro k.
En el caso de cuatro puntos, XA + XB = XC + XD corresponderá a la
intersección de dos familias de elipses.
Nota: Los valores mínimo y máximo de k que
garanticen la existencia de intersección no son sencillos de calcular. Puede
verse un acercamiento en [6].
También se muestra el caso XA + XB = Xr, así como la representación de las
ecuaciones algebraicas correspondientes.
Familias de curvas

En definitiva, el campo a explorar puede ampliarse indefinidamente. Como últimos ejemplos
con distancias, aquí podemos observar algunos resultados con potencias.
Es fácil demostrar que la representación de XA2 + XB2 = k, con k
constante, es una circunferencia centrada en el punto medio de A y B.
Nota: el radio de esa circunferencia es sqrt(k/2 − (x(A-B)/2)²
− (y(A-B)/2)²).
De ello se deduce que el lugar donde la suma de los cuadrados de las
distancias a varios puntos es constante es una circunferencia centrada en
el punto medio de esos puntos.
Además, tomando D = XA2, podemos observar que la representación en el plano real de cualquier polinomio
p(D)
está compuesta exclusivamente por una o más circunferencias.
Nota: se trata de una consecuencia del teorema fundamental del álgebra, ya que
p(D) se puede descomponer en factores (D − c), donde c es un número
complejo. Si
c es real no negativo, entonces D − c = 0 corresponde a una circunferencia de
radio la raíz de c, en caso contrario no se visualiza nada.
Aquí también vemos que podemos representar varias curvas de una misma
familia, como por ejemplo XAn = XB y observar su comportamiento al unísono.
Ángulos
La siguiente es una de las imágenes generada usando el escáner de color
dinámico que más me gustan. El escáner tiene una versatilidad enorme, es
capaz de crear un mapa de calor de prácticamente cualquier situación
[3,
19, 26, 27,
31].

En este caso, se visualiza el primer punto isogónico I1
mediante la intersección de los lugares geométricos que ven bajo el mismo
ángulo a cada par de lados del triángulo.
Nota: I1 coincide con el punto de Fermat cuando el
mayor ángulo del triángulo no supera los 120º; en caso contrario, el punto
de Fermat coincide con el vértice correspondiente a ese ángulo. Se puede
calcular directamente como el centro X(13)
 del triángulo:
del triángulo:
I1 = CentroTriángulo(O, A, B, 13).

Ahora bien, construir el escáner lleva algo de trabajo. Pero podemos usar el CAS para definir no solo distancias, sino también
ángulos. Si alguien continúa pensando que usar la expresión XA en vez de la expresión sqrt((x
− x(A))² + (y − y(A))²) tampoco
ahorra tanto trabajo, tal vez ahora se lo piense mejor al poder usar la
expresión OXA, definida en la vista CAS como:
OXA(x,y):= Ángulo(O, X, A)
en
vez de su equivalente algebraico (siendo O=(a,b) y A=(c,d)):
cos–1((a c – a x + b d – b y – c
x – d y + x² + y²) sqrt(a² c² – 2a² c x + a² d² – 2a² d y + a² x² + a² y²
– 2a c² x + 4a c x² – 2a d² x + 4a d x y – 2a x³ – 2a x y² + b² c² – 2b² c
x + b² d² – 2b² d y + b² x² + b² y² – 2b c² y + 4b c x y – 2b d² y + 4b d
y² – 2b x² y – 2b y³ + c² x² + c² y² – 2c x³ – 2c x y² + d² x² + d² y² –
2d x² y – 2d y³ + x⁴ + 2x² y² + y⁴) / (a² c² – 2a² c x + a² d²
– 2a² d y + a² x² + a² y² – 2a c² x + 4a c x² – 2a d² x + 4a d x y – 2a x³
– 2a x y² +
b² c² – 2b² c x + b² d² – 2b² d y + b² x² + b² y² – 2b c² y + 4b c x y –
2b d² y + 4b d y² – 2b x² y – 2b y³ + c² x² + c² y² – 2c x³ – 2c x y² + d²
x² + d² y² – 2d x² y – 2d y³ + x⁴ + 2x² y² + y⁴))
Naturalmente, esta expresión no es más que un desarrollo deducido del producto escalar
de dos vectores:
vO(x,y):= Vector(X, O)
vA(x,y):= Vector(X, A)
OXA(x,y):= acos((vO vA)/(|vO|*|vA|))
La gran ventaja, además de la comodidad, estriba en que el comando Ángulo nos permite explorar
las relaciones angulares sin necesidad de conocer siquiera las operaciones
básicas con vectores, como el producto escalar.
Aquí podemos ver, por ejemplo, el lugar geométrico correspondiente a los
puntos que forman con el segmento OA un ángulo igual (en radianes) a la
distancia al punto A:
OXA − XA = 0
Nota: las circunferencias cuyos arcos capaces abarcan un
ángulo OXA equivalente a XA radianes tienen por centros:
(O + A)/2 ± VectorNormal(OA)/(2 tg(XA))
Y los que ven los segmentos OA y OB desde el mismo ángulo:
OXA − OXB = 0
Finalmente, la intersección de este último lugar con el correspondiente a la
ecuación OXA – AXB = 0 es el punto de Fermat buscado.
Distancia del Taxi
Nota: esta sección surgió a raíz del confinamiento decretado en España en 2020
debido a la pandemia covid-19. La
Consejería de Educación de Asturias, región donde trabajaba como profesor,
decidió sustituir las clases presenciales por telemáticas, al tiempo que decretó
la obligación de no adelantar materia curricular en ninguna asignatura. Esto me llevó
a buscar un campo de exploración matemática ajeno al currículo oficial pero al
alcance de alumnos de 4º de ESO (de 15 o 16 años). A los alumnos y alumnas les
supuso un aliciente saber que estaban investigando un tema
prácticamente desconocido para la inmensa mayoría de los profesores de
matemáticas. Además, el cambio de métrica conllevó un montón de sorpresas y preguntas.
Una fiesta matemática.
Salgamos ahora de la familiar métrica euclídea:
|
La distancia
del Taxi (o Manhattan) es especialmente sencilla para introducir como
proyecto de investigación en la enseñanza secundaria, ya que su forma
algebraica se reduce a ecuaciones lineales. |
|
Más... |
Distancias de Minkowski
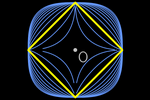
La forma de la circunferencia es determinante en cualquier geometría
plana.
Aquí vemos la definición
de la distancia de Minkowski
 de un punto arbitrario X(x, y) al origen O.
de un punto arbitrario X(x, y) al origen O.
XO(x,y):= (|x|p+|y|p)1/p
Para p=2, tenemos la distancia euclídea.
Para p=1, tenemos la distancia del Taxi.
Variando p, vemos cómo
evoluciona la forma
de la circunferencia
en cada caso.
|
Geometría del Taxi

Efectivamente, como diría Magritte, C'eci n'est pas un disque (esto
no es un disco)
 , pero veremos que sí puede ser la representación de un
círculo si consideramos la métrica del Taxi. , pero veremos que sí puede ser la representación de un
círculo si consideramos la métrica del Taxi.
Usaré los prefijos T y E para distinguir la métrica
del Taxi de
la métrica Euclídea. A la distancia del Taxi aquí la
denominaremos también como distancia taxista.
Nota:
A pesar de que un T-círculo tiene forma cuadrada, seguramente Magritte seguiría afirmando
−con razón− que el T-círculo que vemos es solo una representación, una
imagen del disco; pero además, aquí, al contrario que sucede con una pipa,
el disco representado es una abstracción mental (una forma matemática
ideal) en vez de algo material, por lo que la posible confusión todavía es
mayor.
En la métrica del Taxi (o Manhattan
 )
las distancias se miden en horizontal y vertical, nunca en diagonal. Así,
la T-distancia de un punto arbitrario (x, y) al punto O
es la suma de las diferencias horizontales y verticales, en valor
absoluto, de sus
coordenadas: )
las distancias se miden en horizontal y vertical, nunca en diagonal. Así,
la T-distancia de un punto arbitrario (x, y) al punto O
es la suma de las diferencias horizontales y verticales, en valor
absoluto, de sus
coordenadas:
XO(x,y) := |x – x(O)| + |y – y(O)|
|
Al contrario de lo que sucedía en la métrica euclídea,
GeoGebra no tiene implementado el comando T-distancia, por lo que habremos de
formular "a mano" tanto la distancia entre dos puntos como la distancia
entre punto y recta, facilitándoles ambas fórmulas al alumnado. |
Al igual que GeoGebra representa un segmento ajustándolo a la
cuadrícula de píxeles de la pantalla, podemos imaginar un segmento en diagonal compuesto
de tramos horizontales o verticales tan pequeños como queramos: la
T-distancia entre dos puntos B y C no variará.
La T-distancia entre B y C también será la misma para
cualquier arco creciente o decreciente de una función cuya gráfica vaya de
B a C.
|
En la geometría
del Taxi puede haber infinitos
recorridos mínimos entre dos puntos distintos. |
Todo esto no simplifica la geometría, sino que la complica. Esto se debe a
que la longitud de cada segmento no es uniforme en la dirección, sino que
depende de su pendiente.
En la E-ilusión que se muestra [21], el cuadrado azul parece variar de tamaño, pero solo es un
problema de percepción que desaparece al ver completamente sus lados
(pulsa sobre el cuadrado azul). Explicación: cuando las esquinas son
visibles, estimamos el tamaño del cuadrado por su diagonal; cuando no lo
son, lo valoramos por la distancia entre lados opuestos (longitud del
lado).
Sin embargo, en la geometría del Taxi, el cuadrado azul realmente
varía su área según sea la pendiente de sus lados (mientras que tanto la
T-longitud de sus lados como sus ángulos permanecen constantes).
Analizando el cuadrado en detalle, vemos que el T-perímetro del cuadrado azul y del cuadrado
amarillo es el mismo, pero el área no lo es: El área del cuadrado amarillo
es (b + c)² pero el área del cuadrado azul es b² + c², que es
mínima cuando
b = c. Por lo tanto, en la geometría del Taxi las T-áreas coinciden con las
E-áreas, pero:
|
El área de un T-cuadrado NO es igual, en general, al
cuadrado del lado. |
Podemos imaginar la T-circunferencia como una compresión de la
E-circunferencia. Debido a que la T-longitud no es uniforme en cada
dirección, la T-circunferencia se comprime en una forma cuadrada, con sus
diagonales paralelas a los ejes cartesianos.
T-construcciones básicas
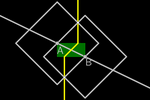
Si fijamos un punto O del plano, podemos considerar la distancia taxista
del resto de los puntos a O.
Como hemos visto, los puntos que T-equidistan de O conforman un cuadrado
(de diagonales paralelas a los ejes). Si el radio es r, el perímetro es
8r, así que la razón entre la T-circunferencia y su T-diámetro es 4 (en
vez de 𝜋).
Al fijar otro punto I distinto de O, establecemos una orientación O→I y
una recta. Tomaremos como unidad la T-distancia de O a I. Podemos seguir pensando en las
T-rectas como si fueran E-rectas, ya que solo cambia el modo de medir cada
segmento. ¡Recordemos que los píxeles obligan a que la propia recta que
dibuja GeoGebra esté formada por tramos horizontales y verticales!
Dado un punto A de la recta r, en esta solo existe otro punto A' a la
misma distancia de O que A. Este T-simétrico coincide con el E-simétrico.
Dados dos puntos distintos A y B, podemos encontrar todos los
que equidistan de ellos.
Esta T-mediatriz no coincide con la euclídea.
Intersecando la T-mediatriz con la recta, obtenemos el punto
medio, que coincide con el punto medio euclídeo.
Las perpendiculares y paralelas son las mismas que en la geometría euclídea,
pero la proyección ortogonal de un punto en una recta no proporciona, en general,
el punto más cercano en la recta. (Es más, "el punto más cercano" tampoco
está unívocamente determinado cuando la recta tiene pendiente 1 o
–1.)
Para hacer una T-inversión
 , llevamos A
e I hasta la horizontal que pasa por O, invertimos (x(A), y(O)) en la E-circunferencia punteada,
de centro O que pasa por (x(I), y(O)), y creamos triángulos
semejantes que garantizan la nueva inversión. , llevamos A
e I hasta la horizontal que pasa por O, invertimos (x(A), y(O)) en la E-circunferencia punteada,
de centro O que pasa por (x(I), y(O)), y creamos triángulos
semejantes que garantizan la nueva inversión.
El T-inverso de A no
coincide con el E-inverso de A.
T-ángulos

En el T-círculo unidad, podemos definir el T-radián exactamente igual que
definimos un E-radián en el E-círculo. Para T-medir un ángulo, basta medir
la T-longitud del arco (rectilíneo) correspondiente en el T-círculo unidad. Un T-círculo tiene 8 T-radianes.
La perpendicularidad y el paralelismo se conservan bajo giros, pero, en
general, las T-distancias no son invariantes ni respecto a E-giros... ¡ni
respecto a T-giros! En efecto, una de las peculiaridades de la T-distancia
es que es sensible a la orientación de las rectas: un segmento, al ser
T-girado, ya no mide igual.

Viñeta de Mafalda, por Quino
La suma de los ángulos de cualquier T-triángulo es de 4 T-radianes. Un
T-triángulo puede ser equilátero o equiángulo, pero nunca puede ser regular.
Cualquier E-cuadrado es también T-cuadrado. Pero como la
distancia taxicab no es uniforme en cualquier dirección, estos dos
T-cuadrados tienen el mismo perímetro (aunque no la misma área):

El cuadrado de la izquierda es, además, un T-círculo.
El de la derecha, no lo es.
Las T-funciones trigonométricas son mucho más sencillas que sus
correspondientes euclídeas. Por ejemplo, la función T-seno no solo no
es trascendente, sino que es lineal a trozos. La función T-tangente, está
formada por E-hipérbolas a trozos.
Nota: Una posible expresión para la función T-seno
es: tsen(x) = 1 – 2 |1/2 - x/4 + 2 floor(1/4 + x/8)|. Así, la
función T-coseno se puede definir como tcos(x) = tsen(x+2). La función
T-tangente es, a trozos, una función homográfica
 . .
T-equidistancias
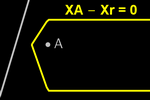
Al contraer las T-circunferencias con el rastro activado, en
cada punto del plano sobrevive el color correspondiente al centro más
cercano.
Con varios puntos, podemos visualizar el diagrama de Voronoi y compararlo con el correspondiente a la distancia euclídea.
Para analizar la equidistancia punto-recta, necesitamos conocer la distancia de
un punto (x, y) a una recta r: a x + b y + c = 0. Tal
distancia es (esta fórmula se proporciona al alumnado y se
puede introducir directamente en la vista algebraica):
Xr(x,y) = |a x + b y + c| / Máximo(|a|, |b|)
De la equidistancia punto-recta surge la T-parábola, mientras que de la
equidistancia punto-circunferencia surgen la T-elipse y la T-hipérbola.
Si consideramos la equidistancia a los lados de un polígono, surge su esqueleto
y su eje medio. Podemos recorrerlo con un disco bitangente para
comprobarlo.
Finalmente, también podemos encontrar el camino T-equidistante entre dos
curvas, ya sea mediante offset (como se muestra aquí) o generando un mapa
de calor.
T-cónicas
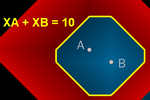
Como ya hemos visto, la T-circunferencia tiene forma
cuadrada (con las diagonales paralelas a los ejes).
La T-elipse tiene forma, en general, de octógono. Si A y B están
en la misma vertical u horizontal, toma forma de hexágono. Cuando la
suma constante coincide con la T-distancia de A a B, la elipse degenera en un
rectángulo de diagonal AB.
La T-parábola está formada, en general, por dos semirrectas
(horizontales o verticales) y dos segmentos.
Por último, cada rama de la T-hipérbola está formada, en general, por dos
semirrectas (horizontales o verticales) y un segmento.
|
Más... |
Combinación lineal T-constante

Al igual que hicimos en la geometría euclídea, podemos generalizar la suma
o diferencia constante a cualquier combinación lineal.
Combinación lineal logarítmica T-constante
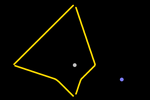
Aquí cabe destacar que las distancias inversamente proporcionales a dos
puntos NO dan lugar a T-circunferencias, como pasaba con la métrica euclídea.
Esto significa que la posible definición de circunferencia
como lugar geométrico de los puntos del plano cuyo cociente de distancias
a dos puntos fijos es constante no es válida para cualquier métrica.
|
T-esfera
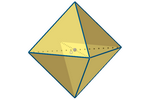
Una T-esfera está formada por los puntos del espacio que T-equidistan de
su centro. Tiene forma de E-octaedro regular (que no es T-regular, pues
los triángulos T-regulares no existen) con sus diagonales paralelas a los
ejes. También se puede generar T-rotando
una T-circunferencia por el diámetro horizontal o vertical.
|
Los lugares geométricos que aparecen en la geometría taxista
invitan a preguntar: ¿qué es lo que tiene que tener "algo" para ser ese
"algo"? ¿Qué caracteriza a un objeto? Por ejemplo, ¿es la E-esfera redonda por
tener sus puntos equidistantes de su centro o lo es por la uniformidad en la dirección que
posee la distancia euclídea? |
T-elipsoide
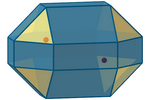
Un T-elipsoide es el lugar geométrico de los puntos del espacio cuya suma
de T-distancias a los focos es constante (k). Tiene, en general, forma de poliedro con 18 caras
rectangulares y 8 caras triangulares (E-regulares pero no T-regulares).
El T-elipsoide degenera en E-cuboctaedro cuando coinciden las diferencias
absolutas de las coordenadas de los focos; degenera en E-cubo cuando esas
diferencias coinciden además con k; y degenera en T-esfera (E-octaedro regular)
cuando los focos coinciden.
Para ciertas posiciones especiales de los focos, aparece un T-elipsoide con todas sus caras
formadas por E-polígonos regulares, pero no es un
E-poliedro regular ni semirregular, pues sus vértices no son uniformes.
Finalmente, cuando la T-distancia entre los focos es igual a k, obtenemos un ortoedro.
Cuerpos
Retornemos a nuestra familiar métrica euclídea. Hasta ahora
hemos usado el álgebra para facilitar la observación de lugares
geométricos. Veamos ahora un ejemplo del proceso recíproco: usar la
geometría para facilitar la observación de estructuras algebraicas.
Normalmente pensamos en las estructuras algebraicas (grupos,
anillos, cuerpos...) como algo inherente a ciertas estructuras numéricas,
como los números enteros o los números reales.
Sin embargo, podemos crear fácilmente estructuras geométricas
equivalentes, con la ventaja de que así podemos visualizar
cada
operación aritmética como una construcción geométrica.
Construcciones preliminares
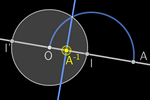
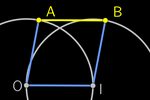
Si fijamos un punto O del plano, podemos considerar la
distancia (euclídea) del resto de los puntos a O. Denotaremos OP a la
distancia de O a P.
Los puntos que equidistan de O conforman una
CIRCUNFERENCIA.
Al fijar otro punto I distinto de O, establecemos una DIRECCIÓN, una
ORIENTACIÓN O→I y una RECTA r.
Tomaremos la distancia OI
como UNIDAD. Además, dos puntos de la recta limitan una
semicircunferencia. Un punto P está en la recta r si cumple alguna de
estas igualdades:
OI = OP + PI (P está entre O e I)
OP = OI + IP (I está entre O y P)
PI = PO + OI (O está entre P e I)
-
Simétrico: Si A está en la recta, en esta solo existe otro
punto A' a la misma distancia de O que A.
Mediatriz: Dados dos puntos distintos A y B, podemos encontrar todos los
que equidistan de ellos.
Punto medio: Intersecando la mediatriz con la recta r, obtenemos el punto
medio MAB.
Perpendicular: La mediatriz nos permite trazar perpendiculares (basta
trazar la circunferencia con centro P a un punto cualquiera de r).
Paralela: Con dos perpendiculares obtenemos una paralela por P a r.
Inversión
 : Con la circunferencia y la perpendicular podemos construir la
inversión de A, A–1. : Con la circunferencia y la perpendicular podemos construir la
inversión de A, A–1.
El cuerpo de los puntos de una recta
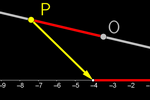
Continuemos con nuestro proceso de construcción de la estructura. Ahora
definiremos las cuatro operaciones elementales.
-
Suma: Para obtener A + B, reflejamos O en MAB obteniendo un nuevo
punto de r.
-
Resta: Para obtener A − B, sumamos A + B'.
-
Multiplicación: Creamos el producto construyendo triángulos
semejantes, obteniendo un nuevo punto de r.
-
División: Para obtener A/B, multiplicamos A x B–1. La división
no es conmutativa.
-
Orden. La simetría I' O I permite definir una RELACIÓN DE ORDEN:
A ≤ O :⇔AI' ≤ AI A ≤ B :⇔A − B ≤ O
Estructura. Por todo lo anterior, el conjunto de los puntos de la recta r,
dotado de las operaciones suma y producto así definidas, constituye una
estructura similar ("cuerpo ordenado") a la de ℝ. De hecho, podemos
establecer una biyección (isomorfismo) entre ambas estructuras:
(r, O, +, ×) → (ℝ, +, ×)
haciendo corresponder a cada punto P de r el número real –OP si P<O y el
número real OP si P≥O.
Nota: Observemos que no entramos en la cuestión, más
espinosa, de cómo construir geométricamente todos los puntos de la recta
(completitud de la recta real). Damos por supuesto que a todo punto le
corresponde un número y viceversa. Ahora bien, si deseamos restringirnos a
los puntos construibles con las operaciones señaladas, podemos establecer
un isomorfismo de esos puntos (ya no sería toda la recta) con el cuerpo de los números
construibles.
|
Los puntos de una recta no son los únicos objetos
geométricos que podemos dotar de la estructura de cuerpo. Nos vale
cualquier otro conjunto de objetos que compartan la misma definición en
la cual solo hay un punto libre residente en una recta.
A continuación, algunos ejemplos. |
|
Más... |
El cuerpo de las mediatrices equidistantes de un
punto fijo y otro libre en una recta fija
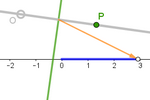
Sea r la recta que pasa por los puntos fijos O e I.
Sea A un punto de r. Llamaremos mA a la mediatriz del segmento OA.
Ahora basta trasladar todas las operaciones ya vistas entre dos puntos A y
B a las correspondientes entre las mediatrices mA y mB.
Si hacemos coincidir el origen de coordenadas con O y el punto
(1,0) con I, al punto P le corresponde (p,0), por lo que podemos
representar la mediatriz mP con la ecuación: x = p/2.
El cuerpo de las parábolas equidistantes de una
recta fija y un punto libre en una recta perpendicular
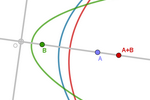
Sea r la recta que pasa por los puntos fijos O e I. Sea la recta d, perpendicular a r por el punto O, y sea A un punto de la
recta r. Llamaremos dA a la
parábola de foco A y directriz d.
Ahora basta trasladar todas las operaciones ya vistas entre dos puntos A y
B a las correspondientes entre las parábolas dA y dB.
Si hacemos coincidir el origen de coordenadas con O
y el punto (1,0) con I, al punto P le corresponderá (p,0), por lo que
podemos representar la parábola dP con la ecuación: y²
= 2p x − p².
El cuerpo de las cónicas equidistantes de una
circunferencia fija y un punto libre en una recta diametral
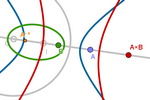
Sea la circunferencia de radio s centrada en O, y sea A un punto de la
recta r que pasa por O e I. Llamaremos sA la cónica de
semieje s y focos O (fijo) y A.
Ahora basta trasladar todas las operaciones ya vistas entre dos puntos A y B
a las correspondientes entre las cónicas sA y sB.
Si hacemos coincidir el origen de coordenadas con O y el punto
(1,0) con I, al punto P le corresponderá (p,0), por lo que podemos
representar la cónica sP con la correspondiente ecuación: (2x-p)²/s²
− 4y²/(p²-s²) = 1.
|
VERSATILIDAD
Listas de poligonales
Las listas permiten agrupar en un solo objeto una gran cantidad de
información. En este ejemplo, las humildes poligonales, que carecen de la elegancia presente en muchas curvas,
la compensan con la versatilidad que les proporciona su agrupación en una
sola lista.
La poligonal cerrada estática
Podemos importar a una hoja de cálculo grandes cantidades de datos.
En este caso, 6122 coordenadas terrestres procedentes de datos públicos de
la North American Cartographic Information Society
 que, una vez depuradas en un procesador de textos y agrupadas debidamente, se convierten en listas.
que, una vez depuradas en un procesador de textos y agrupadas debidamente, se convierten en listas.

Cada
lista de puntos es llamada por el comando Poligonal, de modo que finalmente
obtenemos una lista de poligonales cuyos argumentos son listas de puntos.
Recordemos que, a diferencia del polígono, los vértices de la poligonal no
tienen por qué descansar en el mismo plano. Obtenemos así un único diseño:
el de las costas terrestres. Gracias a este diseño convertimos una anodina
esfera en un modelo de la superficie terrestre.
Costa = {Poligonal((5; 3.142; 1.204), (5; 3.117; 1.211), (5;
3.067; 1.22), (5; 3.031; 1.219), (5; 2.975; 1.223), (5; 2.967; 1.216), (5;
2.981; 1.204), (5; 2.96; 1.199), (5; 2.93; 1.214), (5; 2.896; 1.212), (5;
2.863; 1.216), (5; 2.832; 1.215), (5; 2.809; 1.212), (5; 2.787; 1.217), (5;
2.79; 1.23), (5; 2.775; 1.237), (5; 2.74; 1.24), (5; 2.67; 1.236), (5;
2.624; 1.25), (5; 2.609; 1.26), (5; 2.452; 1.271), (5; 2.429; 1.264), (5;
2.441; 1.248), (5; 2.413; 1.25), (5; 2.4; 1.245), (5; 2.366; 1.251), (5;
2.336; 1.246), (5; 2.308; 1.254), (5; 2.291; 1.236), (5; 2.264; 1.242), (5;
2.242; 1.256), (5; 2.252; 1.264), (5; 2.244; 1.275), ...
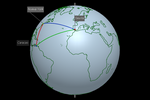
Con ese modelo [16] ya podemos construir un escenario donde podamos realizar
multitud de actividades. Desde observar elementos geográficos (polo, meridiano, paralelo, punto cardinal, ecuador, trópico,
círculo polar, huso, zona horaria...), hasta realizar análisis y
mediciones (octante, latitud, longitud, rumbo, loxodromia, distancias ortodrómicas, triángulo esférico...).
Nota: Este modelo puede servir de excelente ejemplo
del espíritu de colaboración que caracteriza a los recursos creados por la
comunidad GeoGebra desde su inicio. Usándolo como plantilla, Chris Cambré
publicó, en neerlandés e inglés, un libro GeoGebra sobre proyecciones cartográficas
 y otro sobre Mercator
y otro sobre Mercator
 .
Después, Carmen Mathias tradujo ambos al portugués ( .
Después, Carmen Mathias tradujo ambos al portugués ( , ,
 ).
Cerrando el círculo, yo los traduje al español ( ).
Cerrando el círculo, yo los traduje al español ( , ,
 ).
Este comportamiento colaborador adquiere su máxima expresión en el foro de
GeoGebra ).
Este comportamiento colaborador adquiere su máxima expresión en el foro de
GeoGebra
 . .
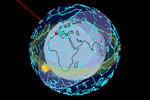 Si ahora añadimos la órbita solar aparente, dispondremos de una
esfera armilar Si ahora añadimos la órbita solar aparente, dispondremos de una
esfera armilar
 (o astrolabio
esférico) que nos permite analizar el paso del tiempo (años, días, horas,
GMT, UTC, estaciones, cénit, oblicuidad de la eclíptica, punto Aries,
equinoccio, solsticio, coordenada celeste, analema, horizonte celeste,
orto, ocaso, las 88 constelaciones, el zodíaco, las estrellas más brillantes...) [20].
(o astrolabio
esférico) que nos permite analizar el paso del tiempo (años, días, horas,
GMT, UTC, estaciones, cénit, oblicuidad de la eclíptica, punto Aries,
equinoccio, solsticio, coordenada celeste, analema, horizonte celeste,
orto, ocaso, las 88 constelaciones, el zodíaco, las estrellas más brillantes...) [20].
Nota: Los datos de la Ascensión Recta y la
Declinación de cada estrella fueron recogidos
aquí.
La poligonal estática autogenerada

A veces podemos ahorrarnos el trabajo de importar los vértices. La
iteración de un guion asociado a un deslizador animado
(desarrollaremos más adelante este procedimiento) permite realizar
fácilmente construcciones en que la lista de vértices de una poligonal se
vaya ampliando sucesivamente por sí misma. Un ejemplo típico de aplicación de este
método es la generación de fractales, como este que muestra el
procedimiento iterativo para la creación del conocido
copo de nieve de Koch y el correspondiente anticopo [29].
FLEXIBILIDAD: Geometría elástica
Geometría elástica
Normalmente, un punto o está o no está en una posición dada. Pero
gracias a los guiones y los vectores podemos flexibilizar esta situación, dotando a los
puntos de la capacidad de moverse libremente y, sin embargo, intentar
mantener en
todo momento cierta relación con otros puntos.
|
En vez de fijar una posición determinada para
cada punto, fijaremos una relación con el resto de puntos. |
Guiones y vectores
Nuestro objetivo es conseguir un polígono equilátero con todos sus
vértices libres. ¿Cómo cerrar la poligonal manteniendo libres sus vértices
(como un metro de carpintero)?
O, partiendo de un polígono: ¿Cómo construir un rombo manteniendo libre el
cuarto vértice?
La solución reside en emplear guiones. Por ejemplo, un punto libre Q
permanecerá en todo momento a 5 unidades
del punto libre P si al actualizar la posición de P se ejecuta el guion:
Valor(Q, P + 5 VectorUnitario(Q−P))
y al actualizar la posición de Q se ejecuta el guion:
Valor(P, Q + 5 VectorUnitario(P−Q))
Así, en un rombo, podemos mantener la distancia entre los vértices A y B
al tiempo que ambos puntos se mantienen libres.
O podemos representar tipos de triángulos (rectángulos, isósceles,
equiláteros...) que mantengan su tipología mientras podemos mover
cualquiera de sus tres vértices.
Este método también sirve para conservar ángulos en vez de distancias.
Basta modificar el vector a aplicar sobre el punto, usando la rotación
adecuada para reajustar el ángulo. Como ejemplo, podemos ver un pentágono
equiángulo con todos sus vértices libres.
Se incluye aquí un resultado (publicado en 2015) que es un bonito ejemplo de
estrecha relación entre geometría y álgebra: "un polígono de n lados es equiangular
si y solo si e2𝜋i/n es una raíz compleja del polinomio de grado n–1 cuyos coeficientes son
las longitudes de los lados consecutivos del polígono"
 . .
Articulaciones
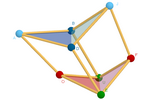
Un ejemplo en el espacio. Esta construcción se basa en el principio
anterior para conservar la distancia (que no los ángulos) de los vértices
de un cubo.
Se obtiene así un cubo articulado, cuyas caras no son necesariamente
planas, sino bisagras de dos triángulos isósceles. Las posibles posiciones
de sus vértices resultan difíciles de analizar sin recurrir a este método
[4, 5, 32].
Guiones de deslizadores animados
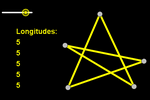
Sin embargo, no podemos generalizar este método a polígonos de más de 4
lados, pues el reajuste de la longitud del quinto lado puede provocar el
desajuste de los ya ajustados. Necesitaríamos un reajuste continuo,
iterativo, hasta conseguir el resultado deseado. Pues bien, podemos
conseguir este reajuste continuo recurriendo a un guion que se ejecuta
continuamente al estar asociado a la actualización del valor de un
deslizador animado.
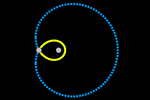
Por ejemplo, en la primera escena parece que P es un punto de la
circunferencia (de radio 4 centrada en A), pero en realidad es un punto libre. Al tirar de él,
volverá a la circunferencia pues se ejecuta permanentemente el guion del
deslizador animado, que es:
Valor(P, P + u)
donde:
u = A - P + 4 VectorUnitario(P
− A)
Podemos añadir un coeficiente (k) para controlar la velocidad: Valor(P, P
+ k u)
Si añadimos otro vector, P se dirigirá hacia la intersección más próxima,
¡incluso aunque no exista intersección!
Haciendo lo mismo con 5 puntos y 5 vectores, voilà! Ya podemos mantener la
equidistancia en más de cuatro puntos.
Fluido

Enmascarando el polígono o la poligonal con curvas, por ejemplo usando splines
 ,
suavizamos la percepción del efecto de la suma de las fuerzas internas (que conservan
la distancia de los puntos) con las externas (que aplican un movimiento al conjunto). ,
suavizamos la percepción del efecto de la suma de las fuerzas internas (que conservan
la distancia de los puntos) con las externas (que aplican un movimiento al conjunto).
Amorfo
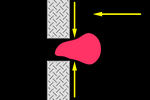
La versatilidad así lograda es grande. Por ejemplo, podemos conseguir, literalmente,
que las figuras "pasen por el aro". Recordemos que en ningún momento se
determina la forma del conjunto, sino que esta es resultado de la suma
vectorial correspondiente a la posición alcanzada en cada instante.
Polígono funicular
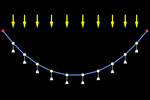
En este ejemplo, partimos de un hilo sin masa apreciable del que cuelgan
pesos (los vértices de la poligonal). El guion asociado al deslizador
animado provoca
que esos vértices se desplacen verticalmente hacia abajo,
simulando la gravedad (fuerza externa), al tiempo que las fuerzas de
cohesión entre los vértices vecinos (fuerzas internas del hilo) limitan ese movimiento.
Como podemos
apreciar, al cabo de pocos segundos la poligonal toma la forma del
polígono funicular
 resultante. Los vértices se ajustan muy bien a una
elipse. Si añadimos más vértices, el ajuste se aproximará más y más a la
parábola teórica
(infinitas cargas puntuales uniformemente distribuidas en horizontal). La catenaria tampoco anda lejos (sería el resultado de
quitar el peso de los vértices y añadir peso uniforme al hilo poligonal:
las cargas se distribuyen uniformemente pero no en horizontal sino a lo
largo de la curva, es decir, separadas por la misma longitud de arco en
vez de por la misma longitud horizontal). resultante. Los vértices se ajustan muy bien a una
elipse. Si añadimos más vértices, el ajuste se aproximará más y más a la
parábola teórica
(infinitas cargas puntuales uniformemente distribuidas en horizontal). La catenaria tampoco anda lejos (sería el resultado de
quitar el peso de los vértices y añadir peso uniforme al hilo poligonal:
las cargas se distribuyen uniformemente pero no en horizontal sino a lo
largo de la curva, es decir, separadas por la misma longitud de arco en
vez de por la misma longitud horizontal).
Newton's Principia
Si hay una rama matemática en donde el álgebra y la geometría
tradicionales se funden de modo natural es en la geometría analítica,
núcleo de los programas de geometría dinámica como GeoGebra.
Uno de los conceptos claves de la geometría analítica es el de
vector. Su
propia representación gráfica, en forma de flecha, invita a pensar en el
movimiento, en el dinamismo. Usaremos los vectores para crear procedimientos dinámicos, muy
sencillos pero a la vez muy potentes, con los que abordar algunas
situaciones.
Suma vectorial

Las agujas de un reloj analógico pueden ser usadas como un ejemplo de
vectores. El extremo de la aguja horaria recorre una circunferencia, al
igual que el extremo del minutero. Si sumamos ambos vectores
obtenemos un lugar geométrico más vistoso (el locus se autointerseca en 11
puntos, siempre que el minutero sea más largo que la aguja horaria, de cada una de 11 direcciones diferentes, lo que significa que en
12 horas la suma vectorial de ambas agujas coincide hasta 121 veces). Si además añadimos el
segundero, la suma vectorial recorre un lugar todavía más complicado.
Las sumas vectoriales abren la puerta a la simulación de equilibrios de
fuerzas. Gracias a los vectores, podemos simular fuerzas, ya sean
atractivas o repulsivas, que obliguen a un punto a tender a ocupar una
posición (o un recorrido) relativamente estable, es decir, equilibrada con
respecto a otras fuerzas o restricciones.
Confinamiento circular entre puntos que se
repelen
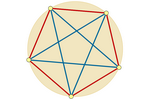
Podemos imaginar los puntos como partículas cargadas
que se repelen entre sí y se encuentran confinadas al mismo círculo. A
cada punto le asociamos la suma de los vectores de repulsión con el resto
de puntos. Así, los puntos se recolocan automáticamente buscando la
posición de equilibrio. Como era de esperar, esta posición corresponde
siempre a los vértices de un polígono regular inscrito en la
circunferencia.
Confinamiento cuadrado entre puntos que se
repelen
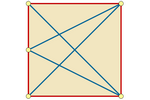
Si cambiamos el círculo por otra figura menos
simétrica, como un cuadrado, ya no son posibles distribuciones regulares
en todos los casos. Sin embargo, la posición de equilibrio se sigue
alcanzando siempre en la frontera perimetral.
Confinamiento esférico entre puntos que se
repelen

Si pasamos del círculo a la esfera (problema de Thomson
 ,
un caso particular de uno de los dieciocho problemas matemáticos no
resueltos propuestos por el matemático Steve Smale ,
un caso particular de uno de los dieciocho problemas matemáticos no
resueltos propuestos por el matemático Steve Smale
 en el año 2000),
la regularidad perfecta ya no es
posible, ya que no existen sólidos platónicos con 5 o 7 vértices, por
ejemplo. en el año 2000),
la regularidad perfecta ya no es
posible, ya que no existen sólidos platónicos con 5 o 7 vértices, por
ejemplo.
Pero, además, ¡tampoco es cierto que el equilibrio se alcance
siempre en la regularidad perfecta! De hecho, con 8 vértices
no es el cubo la configuración que alcanza el equilibrio. Observemos
también que en la mayoría de los casos aparecen poliedros de caras
triangulares (pero en general no equiláteras, por lo que no son deltaedros
 ). ).
Recorrido mínimo
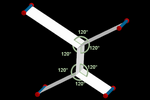
Los vectores que rigen los movimientos de las partículas pueden estar
indefinidos. En cada paso, podemos ensayar con diversos vectores y
quedarnos con aquél que mejor se adapte a nuestro objetivo.
En este
ejemplo, simulación del conocido experimento con película jabonosa, las
partículas prueban varios movimientos antes de decidirse por aquellos que
minimizan la longitud total del perfil y, por tanto, el área total de la superfice
(en este caso, se dirigen a los puntos de Steiner [23]
de los cuatro vértices). Los ángulos de las láminas son de 120º debido a
la uniformidad en la dirección de la distancia euclídea.
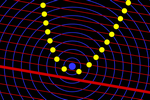
Órbita

Veamos con detalle qué simple es, gracias al deslizador
permanentemente animado, observar el movimiento elíptico de la Tierra
alrededor del Sol sin necesidad de recurrir al análisis infinitesimal [20].
Nota: Esta construcción fue realizada a partir de la
sugerencia de mi compañero de
departamento Julio Valbuena, quien adaptó la idea expuesta por
Richard Feynman en su famoso libro The Feynman Lectures on Physics
(volumen I,
9-7, Planetary motions), ver Bibliografía.
Colocamos el punto S (Sol) en el centro de coordenadas y un punto T
(Tierra) con velocidad inicial el vector v. Si d es la distancia TS y k es
una constante positiva, tenemos el vector de fuerza gravitatoria:
g = k/d² VectorUnitario(S–T)
Ahora solo hay que introducir un deslizador auxiliar para que, cada vez
que se actualice, ejecute el simplísimo guion:
Valor(v, v + 0.03 g)
Valor(T, T + 0.03 v)
¡Y ya tenemos el movimiento elíptico! (Obsérvese que no hemos empleado
ninguna ecuación ni lugar geométrico.)
Caos

La construcción anterior explica las órbitas casi perfectamente elípticas
de los planetas alrededor del sol. El "casi" viene determinado por la
presencia de otros cuerpos. Afortunadamente para los terrícolas, las
órbitas del resto de planetas están suficientemente distantes para que no
trastornen demasiado nuestro año solar. Aquí vemos qué pasaría si no fuese
así. Se trata de una simplificación (dos cuerpos girando alrededor
de otro en el mismo plano) del famoso "problema de los tres cuerpos"
 .
Es impresionante observar cómo una construcción tan simple puede transformar el orden en caos [24]. .
Es impresionante observar cómo una construcción tan simple puede transformar el orden en caos [24].
Burbujas (uso de
JavaScript)

Podemos usar los vectores para modificar el movimiento de un objeto en
función de la distancia que se encuentre de otro, lo que permite, por
ejemplo, detectar colisiones. El problema es que si hay muchos objetos
(n), el número de eventos será elevado, pues crece con el cuadrado del
número de objetos: n(n–1)/2. En estos casos, lo mejor es sustituir los
guiones de GeoGebra por el código JS, más veloz, como se hace en esta
construcción. En ella se muestra el choque elástico, pudiendo
comprobarse la conservación en todo momento de la energía cinética
total.
Tensegridades
La geometría elástica nos permite encontrar situaciones de equilibrio
entre distintas fuerzas. Una aplicación interesante son las estructuras de
tensegridad, compuestas por barras y cables en tensión que las mantienen
unidas.
|
Más... |
Tensegridad
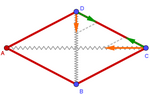
Si conectamos distintos
vértices obtenemos el grafo de una red [25].
Pero si además las conexiones están formadas por barras y
muelles, podemos conseguir que en determinadas posiciones la tensión de
los muelles se equilibre en una estructura estable, denominada tensegridad
 . .
Aquí se muestra un ejemplo en el plano. Gracias a que el rombo es un
paralelogramo, las fuerzas en cada vértice se anulan, de modo que la
estructura se mantiene en equilibrio estable en cualquier posición,
siempre que las tensiones horizontal y vertical sean iguales.
Cálculo de tensiones
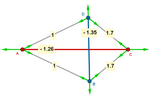
Si ahora partimos de un cuadrilátero cualquiera, la tensegridad
solo se alcanzará para determinadas posiciones y tensiones. Si variamos
alguna de esas posiciones o tensiones, la estructura buscará por sí misma
la nueva posición de equilibrio.
La clave está en los vértices: la suma vectorial de
las fuerzas implicadas ha de ser siempre nula.
|
Tensegridad de prisma triangular
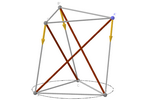
Pasemos al espacio. Una de las tensegridades más sencillas
 parte de un prisma recto cuyas bases son triángulos equiláteros. En sus
aristas laterales colocamos barras y en el resto cables. Si ahora tensamos
los cables, la tensegridad se alcanza cuando una de las bases gira
exactamente 150º con respecto a la otra.
parte de un prisma recto cuyas bases son triángulos equiláteros. En sus
aristas laterales colocamos barras y en el resto cables. Si ahora tensamos
los cables, la tensegridad se alcanza cuando una de las bases gira
exactamente 150º con respecto a la otra.
Tensegridad icosaédrica tensando cables
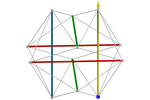
Uno de los padres de las tensegridades, Buckminster Fuller,
mostró especial interés
 por esta tensegridad. Consiste en una estructura formada por tres pares de
barras paralelas, perpendiculares entre sí, tensadas por cables. El
conjunto constituye un icosaedro no convexo, conocido como el icosaedro de Jessen
por esta tensegridad. Consiste en una estructura formada por tres pares de
barras paralelas, perpendiculares entre sí, tensadas por cables. El
conjunto constituye un icosaedro no convexo, conocido como el icosaedro de Jessen
 ,
cuyos vértices no se sitúan en las mismas posiciones que en el icosaedro regular. ,
cuyos vértices no se sitúan en las mismas posiciones que en el icosaedro regular.
Partimos de barras pegadas dos a dos. Al tensar la estructura, las barras
se separan hasta que la dirección de la fuerza resultante
coincida con la de la barra. La proporción entre la longitud de cada barra y cada
cable será entonces de exactamente
.png) (≈1.63). Observemos que en el icosaedro regular tal proporción es la del
número áureo (≈1.62). Podemos observar que el ángulo de las caras del icosaedro de Jessen es de 90º. (≈1.63). Observemos que en el icosaedro regular tal proporción es la del
número áureo (≈1.62). Podemos observar que el ángulo de las caras del icosaedro de Jessen es de 90º.
Tensegridad icosaédrica alargando barras
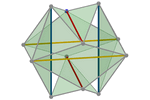
Podemos alcanzar el mismo resultado operando a la inversa. Es decir, en
vez de tensar los cables, intentar alargar lo máximo posible las seis
barras. En este caso partimos de un cuboctaedro. Colocamos las barras y
las estiramos lo máximo posible conservando la longitud original de las
aristas (los cables) del cuboctaedro.
Conclusión
Es cierto que el actual GeoGebra es mucho más complejo que su primera versión de
hace un par de décadas. Contamos con tantos procedimientos y comandos que es
necesaria una planificación previa para decidir, según sea el contexto, cuáles
de ellos realmente necesitamos para alcanzar nuestros objetivos didácticos.
En esta presentación hemos comprobado, con numerosos ejemplos, que GeoGebra
permite afrontar una gran variedad de problemas con un mínimo de medios.
Mientras los comandos CAS hacen posible trascender en algunos casos la
dificultad que supone la introducción del álgebra en la educación secundaria,
las listas, los vectores y los guiones añaden facilidad para representar
situaciones flexibles, dinámicas e interactivas. Y, a menudo, tremendamente
atractivas, tanto en el sentido estético como en el sentido de que invitan a
explorar nuestras propias construcciones (recordemos el efecto Ikea), lo
que favorece la adquisición de la competencia matemática.
Agradecimientos
Aunque en esta
presentación no he pretendido seguir los pasos de las líneas expositivas
realizadas por Tomás Recio en su libro de 1998, Cálculo Simbólico y Geométrico
[30], he de reconocer la enorme
influencia que este libro, que recomiendo vivamente, ha tenido en mi modo
de entender tanto las Matemáticas como su enseñanza. Además,
quiero agradecer a Tomás sus sugerencias y aclaraciones sobre
algunos de los puntos aquí expuestos.
Referencias
[1] Álvarez, J.L. y Losada, R. (2011).
El proyecto
Gauss. Revista SUMA, nº 68, pp. 17-25.
[2] Arranz, J.M., Losada, R., Mora, J.A. y Sada, M. (2008).
El cristo de la farola. Divulgamat, Real Sociedad Matemática
Española. Libro de GeoGebra:
G⁴D en Divulgamat
[3] Arranz, J.M., Losada, R., Mora, J.A. y Sada, M. (2010).
De luz y de color. Divulgamat, Real Sociedad Matemática Española.
Libro de GeoGebra:
G⁴D en Divulgamat
[4] Arranz, J.M., Losada, R., Mora, J.A., Recio, T. y Sada, M. (2009).
GeoGebra on the rocks. Dynamic Geometry Geometry Learn.
[5] Arranz, J.M., Losada, R., Mora, J.A., Recio, T. y Sada, M. (2011).
Modeling the cube using GeoGebra. Model-Centered
Learning: Pathways to mathematical understanding using GeoGebra, pp.
119-131. Eds. L. Bu & R. Schoen (Eds.). Rotterdam: Sense Publishers.
[6] Calatayud, P. (2018).
El problema de la separación de elipses y elipsoides: una aplicación de la
eliminación de cuantificadores.
[7] Hohenwarter, M. (2006).
GeoGebra – didaktische Materialien und Anwendungen
für den Mathematikunterricht.
[8] Kovács, Z.
(2021).
Two almost-circles, and two real ones. Mathematics
in Computer Science 15, pp. 789–801.
[9] Losada, R. (2007).
La chica en
el espejo. Libro de GeoGebra.
[10] Losada, R. (2007).
GeoGebra: la eficiencia de la intución. La Gaceta de la Real Sociedad Matemática
Española, Vol. 10.1, pp. 223-239.
[11] Losada, R. (2009).
GeoGebra en
la Enseñanza de las Matemáticas. Ministerio de Educación y Formación
Profesional. CD-ROM. ISBN: 978-84-369-4794-6.
[12] Losada, R., Recio, T. y Valcarce, J.L. (2009).
Sobre el descubrimiento
automático de diversas generalizaciones del Teorema de Steiner-Lehmus.
Boletín de la Sociedad Puig Adam, nº 82, pp. 53-76. Universidad
Complutense de Madrid. Versión inglesa:
On the automatic discovery of Steiner-Lehmus generalizations.
[13] Losada, R. y Álvarez, J.L. (2010).
GeoGebra en
la Educación
Primaria. Ministerio de Educación y Formación Profesional. CD-ROM.
ISBN: 978-84-369-4909-4.
[14] Losada, R. y Álvarez, J.L. (2011).
Proyecto Gauss.
Instituto de Tecnologías Educativas,
Ministerio de Educación.
[15] Losada, R. (2011).
Dimensiones.
Libro de GeoGebra.
[16] Losada, R. (2011).
Modelos.
Libro de GeoGebra.
[17] Losada, R., Recio, T. y Valcarce, J.L. (2011).
Equal Bisectors at a Vertex of
a Triangle. Computational Science and Its Applications - ICCSA.
[18] Losada, R. y Recio, T. (2011).
Descubrimiento
automático en un problema centenario. La Gaceta de la Real Sociedad Matemática
Española, Vol. 14.4, pp. 693-702.
[19] Losada, R. (2014).
El
color dinámico de GeoGebra. La Gaceta de la Real Sociedad Matemática
Española. Vol. 17 (nº 3), 525–547. Libro de GeoGebra:
Color
dinámico.
[20] Losada, R. (2016).
La Tierra y
el Sol. Libro de GeoGebra. Versión inglesa: Earth and
Sun.
[21] Losada, R. (2017).
La
percepción del tamaño. Libro de GeoGebra.
[22] Losada, R. (2018).
Animaciones
automáticas. Libro de GeoGebra.
[23] Losada, R. (2018).
Autómatas.
Libro de GeoGebra.
[24] Losada, R. (2018).
Billares:
orden y caos. Libro de GeoGebra
[25] Losada, R. y Mora, J.A. (2021).
Redes y grafos. Las comunicaciones y la logística. Exposición
Matemáticas para un mundo mejor. Red DiMa, Día Internacional de las
Matemáticas. Libro de GeoGebra:
Redes y
Grafos.
[26] Losada, R. y Recio, T. (2021).
Mirando a los
cuadros a través de los ojos de Voronoi. Boletín de la
Sociedad Puig Adam, Vol. 112, pp. 32–53. Universidad Complutense de
Madrid. Libro de GeoGebra:
Voronoi
paintings.
[27] Losada, R. (2022).
Mapas de c@lor con GeoGebra. Revista SUMA,
nº 102, pp. 43-57.
Libro de GeoGebra:
Mapas de c@lor
con GeoGebra.
[28] Losada, R. y Recio, T. (2023).
Inclinando la botella de Piaget con
GeoGebra Discovery. Boletín de la
Sociedad Puig Adam, Vol. 115, pp. 43-86. Universidad Complutense de
Madrid. Libro de GeoGebra:
Inclinando
la botella de Piaget con GeoGebra Discovery.
[29] Pérez, A., Sada, M. y Losada, R. (2021).
Fractales, la Geometría del Caos. Exposición Matemáticas para un
mundo mejor. Red DiMa, Día Internacional de las Matemáticas.
[30] Recio, T. (1998).
Cálculo Simbólico y Geométrico, Colección Educación Matemática en
Secundaria, Editorial Síntesis, Madrid.
[31] Recio, T., Losada, R., Kovács, Z. y Ueno, C. (2021).
Discovering
Geometric Inequalities: The Concourse of GeoGebra Discovery, Dynamic
Coloring and Maple Tools. Mathematics 9 (20), 2548.
[32] Recio, T., Losada, R., Tabera, L.F. y Ueno, C. (2022).
Visualizing a Cubic Linkage through the Use of CAS and DGS.
Mathematics 2022, 10(15),
2550; https://doi.org/10.3390/math10152550. Libro de GeoGebra:
Mecanismos. Versión inglesa:
Linkages.
Bibliografía
-
Arranz, J.M., Losada, R., Mora, J.A. y Sada, M. (2008).
Arcos con geometría dinámica. Matematicalia, Real Sociedad
Matemática Española, Vol. 4.1. Libro de GeoGebra:
Arte
y Geometría: Arcos
-
Arranz, J.M., Losada, R., Mora, J.A. y Sada, M. (2008).
Conjeturas a partir de los puntos medios. Divulgamat, Real Sociedad
Matemática Española. Libro de GeoGebra:
G⁴D en Divulgamat
-
Arranz, J.M., Losada, R., Mora, J.A. y Sada, M. (2008).
La percepción tridimensional. Divulgamat, Real Sociedad Matemática
Española. Libro de GeoGebra:
G⁴D en Divulgamat
-
Arranz, J.M., Losada, R., Mora, J.A. y Sada, M. (2008).
Geometría en rosetones góticos. Divulgamat, Real Sociedad
Matemática Española. Libro de GeoGebra:
G⁴D en Divulgamat
-
Arranz, J.M., Losada, R., Mora, J.A. y Sada, M. (2009).
Mosaicos con GeoGebra. Colección Lemniscata, nº 7, pp. 57-87. Editorial
Anaya. Libro de GeoGebra:
Arte y Geometría: Mosaicos
-
Arranz, J.M., Losada, R., Mora, J.A. y Sada, M. (2009).
Realities from GeoGebra. MSOR Connections Vol 9 No 2. Versión
española:
Realidades de GeoGebra Revista SUMA, nº 67, pp. 7-20.
Reeditado con ocasión del
nº 100 en 2022. Libro de GeoGebra:
Realidades
de GeoGebra.
-
Botana, F., Kovács, Z., Recio, T. y Vélez, M.P. (2020).
Hacia
un autómata geómetra. La Gaceta de la Real Sociedad Matemática
Española, Vol. 23.2, pp. 343–371
-
Burkhardt, R.W. (2008).
A Practical Guide to Tensegrity Design.
-
Carrillo, A. y Recio, T. (2020).
De Curva a Curva,
con GeoGebra. Boletín de la
Sociedad Puig Adam, nº 110.
-
Durán, A.J., Mora, J.A., Pereiro, D., Losada, R., Muñoz, J.L., Arranz, J.M.
(2021).
Matemáticas y belleza. Exposición Matemáticas para un
mundo mejor. Red DiMa, Día Internacional de las Matemáticas.
-
Feynman, R., Leighton, R.B. y Sands, M. (1963).
The Feynman Lectures on Physics, Mainly Mechanics, Radiations and Heat,
Volume I. Addison-Wesley.
-
Goicolea, J.M. (2021).
Cálculo de Cables. Universidad Politécnica de Madrid.
-
de Guzmán, M. (2002).
Tensegridad. De la escultura a la célula. Ars Medica. Revista de
Humanidades.
-
Losada, R. (2002).
All Lights y Lights Out: una investigación entre luces y sombras.
Revista SUMA, nº 40, pp. 25-41. Libro de GeoGebra:
Juegos de
iluminación (con soluciones). Versión inglesa:
Lights Out (games with solutions).
-
Losada, R. (2010).
Isometrías. Libro de GeoGebra.
-
Losada, R. (2010).
Estadística
y Probabilidad. Libro de GeoGebra.
-
Losada, R. (2011).
Aritmética y
cálculo mental. Libro de GeoGebra.
-
Losada, R. (2011).
Ecuaciones y
sistemas. Libro de GeoGebra.
-
Losada, R. (2011).
Funciones. Libro de GeoGebra.
-
Losada, R. (2011).
Música y
matemáticas. Divulgamat, Real Sociedad Matemática
Española. Libro de GeoGebra:
Música y
Matemáticas
-
Losada, R. y Álvarez, J.L. (2011).
Los applets de funciones en el Proyecto Gauss. Revista UNO,
nº 58, pp. 25-37. Editorial Graó.
-
Losada, R. y
Álvarez, J.L. (2012).
Estadística y probabilidad en el Proyecto Gauss. Revista UNO,
nº 59, pp. 26-39. Editorial Graó.
-
Losada, R. y
Álvarez, J.L. (2012).
La hoja de cálculo de GeoGebra. Revista UNO,
nº 61, pp.
55-66. Editorial Graó.
-
Losada, R.
(2016).
Geogebra en el aula, un descubrimiento gradual. Revista UNO, nº 71, pp. 13-19. Editorial Graó.
-
Losada, R. (2021).
Cambio de
sistema de referencia. Libro de GeoGebra.
-
Losada, R. (2021).
Variable
compleja. Libro de GeoGebra.
-
Losada, R. (2021).
Julia y
Mandelbrot. Libro de GeoGebra.
-
Petrovic, M., Malesevic, B., Banjac, B. y Obradovic, R. (2014).
Geometry of some
taxicab curves.
-
Plaza, S. y
Gutiérrez, J.M. (2013).
Dinámica del método de Newton.
Universidad de La Rioja.
-
Ramellini, G.,
Losada, R. y Muñoz, J. (2021).
Juegos y Matemáticas. Exposición Matemáticas para un mundo mejor.
Red DiMa, Día Internacional de las Matemáticas. Libros de GeoGebra:
Juegos,
Rompecabezas,
Matemágicas.
-
San Segundo, F. (2010).
Effective
algorithms for the study of the degree of algebraic varieties in
offsetting processes.
|
|
![]()
![]()